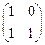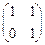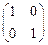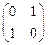题目内容
行列式
(A>0)按第一列展开得
M11-2M21+M31,记函数f(x)=M11+M21,且f(x)的最大值是4.
(1)求A;
(2)将函数y=f(x)的图象向左平移
个单位,再将所得图象上各点的横坐标扩大为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)在(-
,
)上的值域.
| . |
| . |
| 3 |
(1)求A;
(2)将函数y=f(x)的图象向左平移
| π |
| 12 |
| π |
| 12 |
| 11π |
| 12 |
(1)由题意,M11=
=Asinxcosx=
sin2x,M21=-
=-Acos2x+
=-
cos2x…(2分)
∴f(x)=
sin2x-
cos2x=
sin(2x-
)…(3分)
∴fmax=
=4,∴A=4
…(1分)
(2)向左移
得y=4sin(2x-
),…(2分)
横坐标变为原来2倍得g(x)=4sin(x-
)…(1分)
∵x∈(-
,
),∴x-
∈(-
,
)…(1分)
∴g(x)=4sin(x-
)∈(-2,4]…(3分)
| . |
| . |
| A |
| 2 |
| . |
| . |
| A |
| 2 |
| A |
| 2 |
∴f(x)=
| A |
| 2 |
| A |
| 2 |
| ||
| 2 |
| π |
| 4 |
∴fmax=
| ||
| 2 |
| 2 |
(2)向左移
| π |
| 12 |
| π |
| 12 |
横坐标变为原来2倍得g(x)=4sin(x-
| π |
| 12 |
∵x∈(-
| π |
| 12 |
| 11π |
| 12 |
| π |
| 12 |
| π |
| 6 |
| 5π |
| 6 |
∴g(x)=4sin(x-
| π |
| 12 |

练习册系列答案
相关题目
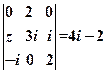 (
(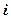 为虚数单位),则复数
为虚数单位),则复数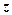 =_______.
=_______.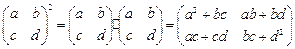 . 则
. 则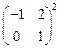 为
为