题目内容
已知抛物线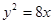 与椭圆
与椭圆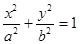 有公共焦点
有公共焦点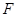 ,且椭圆过点
,且椭圆过点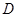
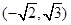 .
.
(1)求椭圆方程;
(2)点 、
、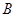 是椭圆的上下顶点,点
是椭圆的上下顶点,点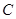 为右顶点,记过点
为右顶点,记过点 、
、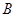 、
、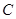 的圆为⊙
的圆为⊙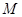 ,过点
,过点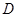 作⊙
作⊙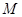 的切线
的切线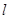 ,求直线
,求直线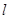 的方程;
的方程;
(3)过椭圆的上顶点作互相垂直的两条直线分别交椭圆于另外一点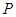 、
、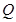 ,试问直线
,试问直线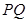 是否经过定点,若是,求出定点坐标;若不是,说明理由.
是否经过定点,若是,求出定点坐标;若不是,说明理由.
(1)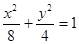 ;(2)
;(2)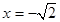 或
或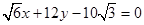 ;(3)
;(3)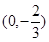 .
.
解析试题分析:(1)由题目给出的条件直接求解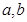 的值,则可求出椭圆方程;(2)当所求直线斜率不存在时,其方程为
的值,则可求出椭圆方程;(2)当所求直线斜率不存在时,其方程为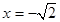 ,符合题意;当直线斜率存在时,可设其斜率为
,符合题意;当直线斜率存在时,可设其斜率为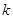 ,写出直线的点斜式方程,因为直线与圆相切,所以根据圆心到直线的距离等于圆的半径可直接求得直线的斜率,从而得到方程;(3)由题意可知,两直线的斜率都存在,设AP:
,写出直线的点斜式方程,因为直线与圆相切,所以根据圆心到直线的距离等于圆的半径可直接求得直线的斜率,从而得到方程;(3)由题意可知,两直线的斜率都存在,设AP: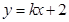 ,代入椭圆的方程从而求出点
,代入椭圆的方程从而求出点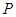 的坐标,同理再求出点
的坐标,同理再求出点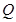 的坐标,从而可求出直线
的坐标,从而可求出直线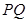 的方程,由方程可知当
的方程,由方程可知当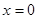 时,
时,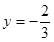 恒成立,所以直线恒过定点
恒成立,所以直线恒过定点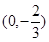 .
.
试题解析:
(1)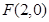 ,则c=2, 又
,则c=2, 又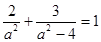 ,得
,得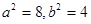
∴所求椭圆方程为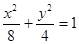 .
.
(2)M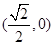 ,⊙M:
,⊙M: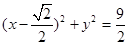 ,直线l斜率不存在时,
,直线l斜率不存在时,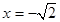 ,
,
直线l斜率存在时,设为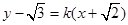 ,
,
∴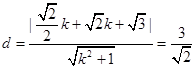 ,解得
,解得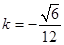 ,
,
∴直线l为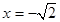 或
或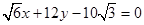 .
.
(3)显然,两直线斜率存在, 设AP: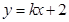 ,
,
代入椭圆方程,得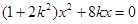 ,解得点
,解得点 ,
,
同理得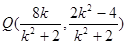 ,直线PQ:
,直线PQ: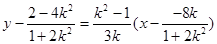 ,
,
令x=0,得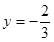 ,∴直线PQ过定点
,∴直线PQ过定点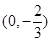 .
.
考点:本题考查了椭圆的标准方程,考查了椭圆的简单几何性质,考查了直线和圆锥曲线的关系,突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
相关题目
 是多少?
是多少?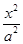 +
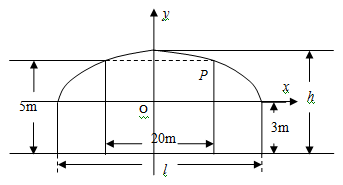
+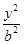 =1的面积公式为S=
=1的面积公式为S=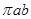 ,柱体体积为底面积乘以高。)
,柱体体积为底面积乘以高。)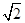 倍,试确定M、N的位置以及
倍,试确定M、N的位置以及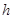 的值,使总造价最少。
的值,使总造价最少。 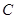 的中心在原点
的中心在原点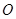 ,离心率
,离心率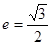 ,右焦点为
,右焦点为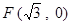 .
.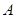 ,在椭圆
,在椭圆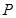 ,使得向量
,使得向量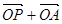 与
与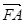 共线?若存在,求直线
共线?若存在,求直线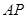 的方程;若不存在,简要说明理由.
的方程;若不存在,简要说明理由.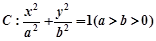 的焦点为
的焦点为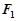
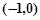 ,
,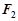
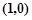 ,且经过点
,且经过点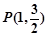 .
. 的方程;
的方程; 与椭圆
与椭圆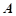 、
、 两点,问在椭圆
两点,问在椭圆 ,使四边形
,使四边形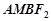 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线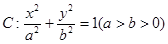 过点
过点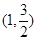 ,且离心率
,且离心率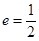 。
。 的标准方程;
的标准方程;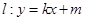 与椭圆
与椭圆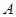 ,
,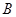 两点(
两点(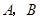 不是左右顶点),椭圆的右顶点为D,且满足
不是左右顶点),椭圆的右顶点为D,且满足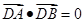 ,试判断直线
,试判断直线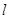 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。
是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。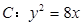 ,
,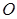 为坐标原点,动直线
为坐标原点,动直线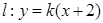 与
与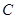 交于不同两点
交于不同两点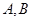
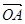 ·
·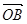 为常数;
为常数;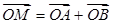 的点
的点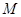 的轨迹方程。
的轨迹方程。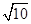 时,求k的值.
时,求k的值. 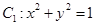 在矩阵
在矩阵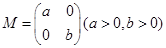 的变换作用下得到曲线
的变换作用下得到曲线 .
.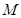 ;
;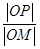 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.