题目内容
已知抛物线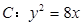 ,
,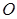 为坐标原点,动直线
为坐标原点,动直线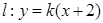 与
与
抛物线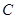 交于不同两点
交于不同两点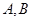
(1)求证: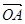 ·
·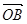 为常数;
为常数;
(2)求满足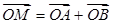 的点
的点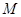 的轨迹方程。
的轨迹方程。
(1)略(参考解析);(2) .
.
解析试题分析:(1)抛物线与直线联立.由向量的数量积结合利用韦达定理可得结论.(2)根据向量的相等得到点M关于A,B两点的坐标关系,再由第一步的韦达定理消去k值即可.但要注意轨迹的范围.本题主要就是抛物线与直线的知识.向量知识在解析几何中的应用.
试题解析:解:将 代入
代入 ,整理得
,整理得 ,
,
因为动直线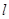 与抛物线C交于不同两点A、B,所以
与抛物线C交于不同两点A、B,所以 且
且 ,即
,即
解得:  且
且 .
.
设 ,
, ,则
,则 .
.
(1)证明: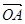 ·
·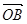

= =
=
∴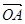 ·
·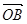 为常数.
为常数.
(2)解:

 .
.
设 ,则
,则 消去
消去 得:
得:  .
.
又由 且
且 得:
得: ,
,  , ∴
, ∴ ,
,
所以,点 的轨迹方程为
的轨迹方程为 .
.
考点:1.抛物线与直线的关系.2.向量的和差知识.3.关注轨迹的范围.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
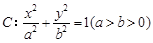 的离心率为
的离心率为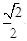 ,其中左焦点
,其中左焦点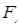 (-2,0).
(-2,0).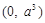 的两直线与抛物线
的两直线与抛物线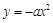 相切于A、B两点, AD、BC垂直于直线
相切于A、B两点, AD、BC垂直于直线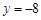 ,垂足分别为D、C.
,垂足分别为D、C.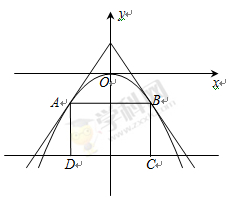
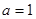 ,求矩形ABCD面积;
,求矩形ABCD面积;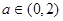 ,求矩形ABCD面积的最大值.
,求矩形ABCD面积的最大值. 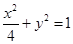 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
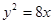 与椭圆
与椭圆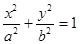 有公共焦点
有公共焦点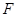 ,且椭圆过点
,且椭圆过点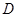
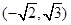 .
. 、
、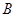 是椭圆的上下顶点,点
是椭圆的上下顶点,点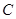 为右顶点,记过点
为右顶点,记过点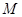 ,过点
,过点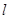 ,求直线
,求直线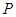 、
、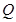 ,试问直线
,试问直线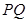 是否经过定点,若是,求出定点坐标;若不是,说明理由.
是否经过定点,若是,求出定点坐标;若不是,说明理由.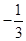 .
.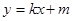 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证: 直线l过定点,并求出该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证: 直线l过定点,并求出该定点的坐标. 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证: 直线l过定点,并求出该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点。求证: 直线l过定点,并求出该定点的坐标.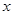 轴上,离心率
轴上,离心率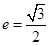 ,点
,点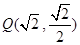 在椭圆C上.
在椭圆C上.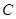 的标准方程;
的标准方程;
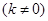 的直线
的直线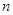 交椭圆
交椭圆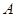 、
、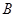 两点,且
两点,且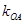 、
、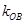 成等差数列,点M(1,1),求
成等差数列,点M(1,1),求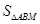 的最大值.
的最大值.