题目内容
6.设O为坐标原点,直线l:x-y+m=0与圆C:x2-2x+y2-7=0交于M,N两点,与x轴,y轴交于A,B两点,且$\sqrt{3}$|$\overrightarrow{MN}$|=3|$\overrightarrow{OM}$+$\overrightarrow{ON}$|,点P在直线l上,满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,若$\overrightarrow{PO}$•$\overrightarrow{PC}$=3,则λ的值为4±$\sqrt{17}$或-3$±\sqrt{10}$.分析 设M(x1,y1),N(x2,y2),联立直线方程和圆方程,运用韦达定理,以及向量的加法运算和模的公式,以及弦长公式,可得m的方程,解方程可得m的值,分别讨论m的值,设出P的坐标,求得A,B,C的坐标,运用向量的坐标运算和数量积的坐标表示,解方程即可得到所求值.
解答 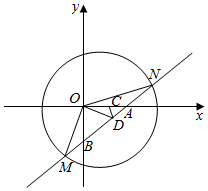 解:设M(x1,y1),N(x2,y2),
解:设M(x1,y1),N(x2,y2),
由$\left\{\begin{array}{l}{x-y+m=0}\\{{x}^{2}-2x+{y}^{2}-7=0}\end{array}\right.$得2x2+(2m-2)x+m2-7=0,
∴x1+x2=1-m,y1+y2=1+m,
$\overrightarrow{OM}+\overrightarrow{ON}=(1-m,1+m)$,则|$\overrightarrow{OM}$+$\overrightarrow{ON}$|=$\sqrt{2+2{m}^{2}}$,
圆心C到MN的距离d2=$\frac{(1+m)^{2}}{2}$,
|$\overrightarrow{MN}$|2=4(r2-d2)=4(8-d2),
由|$\overrightarrow{MN}$|2=3|$\overrightarrow{OM}$+$\overrightarrow{ON}$|2得3m2+2d2=13,
⇒2m2+m-6=0,解得m=-2或m=$\frac{3}{2}$,
当m=-2时,设P(x,x-2),A(2,0),B(0,-2),C(1,0),
由$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,$\overrightarrow{PO}$•$\overrightarrow{PC}$=3,
可得(x-2,x-2)=λ(-x,-x),即有x-2=-λx,
(-x,2-x)•(1-x,2-x)=3,即有-x(1-x)+(2-x)2=3,
化为2x2-5x+1=0,
解得x=$\frac{5±\sqrt{17}}{4}$,λ=4±$\sqrt{17}$;
当m=$\frac{3}{2}$时,设P(x,x+$\frac{3}{2}$),A(-$\frac{3}{2}$,0),B(0,$\frac{3}{2}$),C(1,0),
由$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,$\overrightarrow{PO}$•$\overrightarrow{PC}$=3,
可得(x+$\frac{3}{2}$,x+$\frac{3}{2}$)=λ(-x,-x),即有x+$\frac{3}{2}$=-λx,
(-x,-$\frac{3}{2}$-x)•(1-x,-$\frac{3}{2}$-x)=3,即有-x(1-x)+(-$\frac{3}{2}$-x)2=3,
化为2x2+2x-$\frac{3}{4}$=0,
解得x=$\frac{-2±\sqrt{10}}{4}$,λ=-3$±\sqrt{10}$.
综上可得,λ=4±$\sqrt{17}$或λ=-3$±\sqrt{10}$.
故答案为:4±$\sqrt{17}$或-3$±\sqrt{10}$.
点评 本题考查直线和圆的位置关系,考查方程思想和向量的坐标运算和数量积的坐标表示,考查运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| 无意愿 | 有意愿 | 总计 | |
| 男 | a | b | 40 |
| 女 | 5 | d | A |
| 总计 | 25 | B | 80 |
(Ⅱ)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
| A. | 1 | B. | 2 | C. | 1$+\sqrt{3}$ | D. | -2 |
| A. | y=-$\frac{1}{x}$ | B. | y=x3+x | C. | y=-x|x| | D. | y=ln$\frac{1+x}{1-x}$ |
 如图,椭圆C:x2+3y2=3b2(b>0)
如图,椭圆C:x2+3y2=3b2(b>0)