题目内容
设f（x）=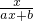
（a，b为非零常数）满足f（2）=1，f（x）=x有唯一解，求函数y=f（x）的解析式和f[f（-3）]的值．
解：∵f（2）=1，
∴
=1，即2a+b=2．①
又∵f（x）=x有唯一解，
即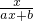=x有唯一解，
∴x•
=0有唯一解．
而x1=0，x2=
，
∴=0．②
由①②知a=
，b=1．
∴f（x）=
=
．
∴f[f（-3）]=f
=f（6）=
=
．
分析：利用已知条件列出关于字母a，b的方程组，通过求解方程组确定出函数的解析式．注意待定系数法的运用，先计算出f（-3），再求出f[f（-3）]的值．
点评：本题考查函数解析式的求解，考查方程思想．考查二次方程有等根的条件．注意待定系数法的运用，考查运算能力．
∴
=1，即2a+b=2．①又∵f（x）=x有唯一解，
即
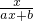=x有唯一解，∴x•
=0有唯一解．而x1=0，x2=
，∴
=0．②由①②知a=
，b=1．∴f（x）=
=．∴f[f（-3）]=f
=f（6）==．分析：利用已知条件列出关于字母a，b的方程组，通过求解方程组确定出函数的解析式．注意待定系数法的运用，先计算出f（-3），再求出f[f（-3）]的值．
点评：本题考查函数解析式的求解，考查方程思想．考查二次方程有等根的条件．注意待定系数法的运用，考查运算能力．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目