题目内容
已知函数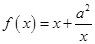 ,
,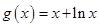 ,其中
,其中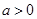 .
.
(1)若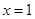 是函数
是函数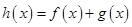 的极值点,求实数
的极值点,求实数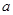 的值;
的值;
(2)若对任意的 (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数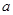 的取值范围.
的取值范围.
(1) ;(2)
;(2)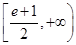 .
.
解析试题分析:(1)由连续可导函数在极值点处的导数为0求出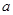 的值,再验证充分性即可,这里容易忘记验证充分性,一定要注意连续可导函数在某点处导数为0,只是在该处取得极值的必要条件,而非充要条件;(2)条件等价转化为
的值,再验证充分性即可,这里容易忘记验证充分性,一定要注意连续可导函数在某点处导数为0,只是在该处取得极值的必要条件,而非充要条件;(2)条件等价转化为 ,然后以导数为工具,求出分别求出
,然后以导数为工具,求出分别求出 ,通过解不等式可得实数
,通过解不等式可得实数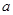 的取值范围,注意分类讨论.本小题要注意是
的取值范围,注意分类讨论.本小题要注意是 两个相互独立的变量,没有约束关系,所能转化为
两个相互独立的变量,没有约束关系,所能转化为 , 若题目改为“若对任意的
, 若题目改为“若对任意的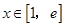 都有
都有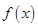 ≥
≥ 成立”,则可考虑转化为
成立”,则可考虑转化为 成立去解答.
成立去解答.
试题解析:(1)解法1:∵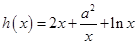 ,其定义域为
,其定义域为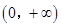 , 1分
, 1分
∴ .3分
.3分
∵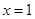 是函数
是函数 的极值点,∴
的极值点,∴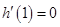 ,即
,即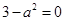 .
.
∵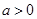 ,∴
,∴ .
.
经检验当 时,
时,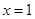 是函数
是函数 的极值点,∴
的极值点,∴ . 5分
. 5分
解法2:∵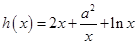 ,其定义域为
,其定义域为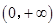 ,
,
∴ . 令
. 令 ,即
,即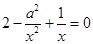 ,整理,得
,整理,得 .
.
∵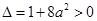 ,
,
∴ 的两个实根
的两个实根 (舍去),
(舍去),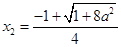 ,
,
当 变化时,
变化时, ,
,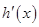 的变化情况如下表:
的变化情况如下表:
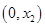
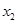

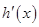
— 0 + 

极小值 

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
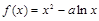 (
(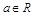 )。
)。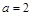 ,求证:
,求证: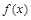 在
在 上是增函数;
上是增函数; 上的最小值。
上的最小值。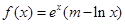 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数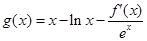 的最小值为1,其中
的最小值为1,其中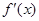 是函数f(x)的导数.
是函数f(x)的导数. .
.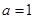 时,求函数
时,求函数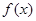 的极值;
的极值;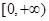 上单调递增,试求
上单调递增,试求 的取值或取值范围
的取值或取值范围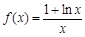 .
. 上存在极值,求实数
上存在极值,求实数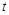 的取值范围;
的取值范围;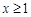 时,不等式
时,不等式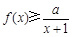 恒成立,求实数
恒成立,求实数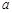 的取值范围.
的取值范围. ,
, 为函数
为函数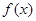 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. ,
,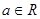
 时,求曲线
时,求曲线 在点
在点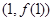 处的切线方程;
处的切线方程;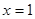 处有极值,求
处有极值,求 ,使
,使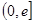 的最小值是3,若存在,求出
的最小值是3,若存在,求出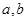 是实数,函数
是实数,函数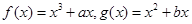 ,
,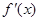 和
和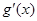 ,分别是
,分别是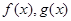 的导函数,若
的导函数,若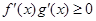 在区间
在区间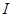 上恒成立,则称
上恒成立,则称 和
和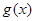 在区间
在区间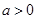 ,若函数
,若函数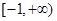 上单调性一致,求实数
上单调性一致,求实数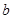 的取值范围;
的取值范围;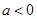 且
且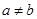 ,若函数
,若函数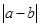 的最大值.
的最大值.