题目内容
(2011·高考课标全国卷)如图 ,四棱锥P
,四棱锥P -ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. 
(1)证明:PA⊥BD;
(2)设PD=AD=1,求棱锥D-PBC的高.
解:(1)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=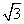 AD.
AD.
所以BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,所以BD⊥PD.
所以BD⊥平面PAD,故PA⊥BD.
(2)
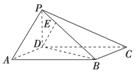
如图,作DE⊥PB,垂足为E.
已知PD⊥底面ABCD,故PD⊥BC.
由(1)知BD⊥AD,
因为BC∥AD,
所以BC⊥BD.
所以BC⊥平面PBD,BC⊥DE.
则DE⊥平面PBC,即DE为棱锥D-PBC的高.
由PD=AD=1知BD=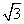 ,PB=2.
,PB=2.
由DE· PB=PD·BD得DE=
PB=PD·BD得DE=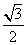 ,
,
所以棱锥D-PBC的高为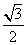 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
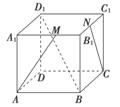
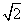 .将△ABD沿矩形的对角线BD所在
.将△ABD沿矩形的对角线BD所在

 .x和y的相关系数为直线l的斜率
.x和y的相关系数为直线l的斜率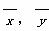 )
)