题目内容
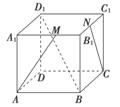
如图所示，正方体ABCD－A1B1C1D1中，M、N分别是A1B1、B1C1的中点．问：
(1)AM和CN是否是异面直线？说明理由；
(2)D1B和CC1是否是异面直线？说明理由．
解：
(1)不是异面直线．理由如下：
连接MN、A1C1、AC.
∵M、N分别是A1B1、B1C1的中点，
∴MN∥A1C1.
又∵A1A綊C1C，
∴A1ACC1为平行四边
形，
∴A1C1∥AC，∴MN∥AC，
∴A、M、N、C在同一平面内，故AM和CN不是异面直线．
(2)是异面直线．证明如下：
∵ABCD－A1B1C1D1是正方体，
∴B、C、C1、D1不共面．
假设D1B与CC1不是异面直线，
则存在平面α，使D1B⊂平面α，CC1⊂平面α，
∴D1、B、C、C1∈α，与ABCD－A1B1C1D1是正方体矛盾．
∴假设不成立，即D1B与CC1是异面直线．
练习册系列答案
阅读快车系列答案
相关题目
C中，AB⊥AC，AD⊥BC于D，求证：
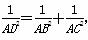，那么在四面体A－BCD中，类比上述结论，你能得到怎样的猜想？并说明理由．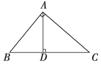
C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D的体积为________cm3.
，DA⊥AC，DA⊥AB，若DA＝1，且E为DA的中点．求异面直线BE与CD所成角的余弦值．
，四棱锥P