题目内容
函数y=sin2x+2cosx(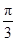 ≤x≤
≤x≤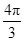 )的最大值与最小值分别为( )
)的最大值与最小值分别为( )
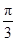 ≤x≤
≤x≤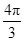 )的最大值与最小值分别为( )
)的最大值与最小值分别为( )A.最大值为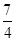 ,最小值为- ,最小值为-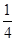 |
B.最大值为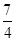 ,最小值为-2 ,最小值为-2 |
C.最大值为2,最小值为-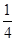 |
| D.最大值为2,最小值为-2 |
B
化简函数y=sin2x+2cosx(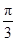 ≤x≤
≤x≤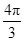 )得y=-cos2x+2cosx+1=-(cosx-1)2+2,
)得y=-cos2x+2cosx+1=-(cosx-1)2+2,
当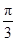 ≤x≤
≤x≤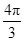 时,
时,
cosx∈[-1, ],
],
故函数的最小值在cosx=-1时取得为-2,
最大值在cosx= 时取得为
时取得为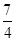 .
.
故选B.
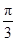 ≤x≤
≤x≤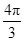 )得y=-cos2x+2cosx+1=-(cosx-1)2+2,
)得y=-cos2x+2cosx+1=-(cosx-1)2+2,当
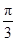 ≤x≤
≤x≤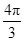 时,
时,cosx∈[-1,
 ],
],故函数的最小值在cosx=-1时取得为-2,
最大值在cosx=
 时取得为
时取得为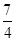 .
.故选B.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
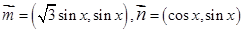 ,函数
,函数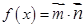 .
. 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;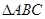 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
,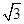 ,sinx),x∈R.
,sinx),x∈R.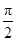 ),证明:a和b不平行;
),证明:a和b不平行;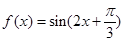 ,则下列结论正确的是
,则下列结论正确的是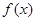 的图像关于直线
的图像关于直线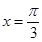 对称
对称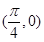 对称
对称 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像 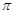 ,且在
,且在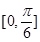 上为增函数
上为增函数 )(
)(



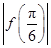 对一切x∈R恒成立,则
对一切x∈R恒成立,则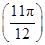 =0;
=0;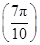 ︱<︱f
︱<︱f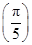 ︱;
︱; 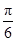 ,kπ+
,kπ+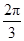 ](k∈Z);
](k∈Z); )在区间[0,
)在区间[0, ]上的最小值为( )
]上的最小值为( )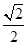
 sinxcosx+1.
sinxcosx+1.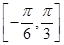 ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.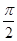 ,直线x=
,直线x=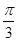 是其图象的一条对称轴,则下面各式中符合条件的解析式为 ( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为 ( )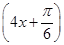
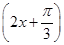 +2
+2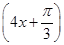 +2
+2