题目内容
已知a=(5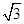 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+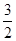 .
.
(1)当∈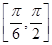 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当x∈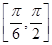 时,若f(x)=8,求函数f
时,若f(x)=8,求函数f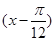 的值;
的值;
(3)将函数y=f(x)的图象向右平移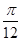 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
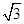 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+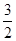 .
.(1)当∈
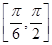 时,求函数f(x)的值域;
时,求函数f(x)的值域;(2)当x∈
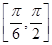 时,若f(x)=8,求函数f
时,若f(x)=8,求函数f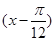 的值;
的值;(3)将函数y=f(x)的图象向右平移
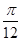 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.(1) (2)
(2) +7(3)g(x)=5sin 2x,g(x)为奇函数
+7(3)g(x)=5sin 2x,g(x)为奇函数
 (2)
(2) +7(3)g(x)=5sin 2x,g(x)为奇函数
+7(3)g(x)=5sin 2x,g(x)为奇函数(1)f(x)=a·b+|b|2+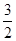
=5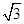 sin xcos x+2cos2x+4cos2x+sin2x+
sin xcos x+2cos2x+4cos2x+sin2x+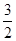 =5
=5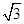 sin xcos x+5cos2x+
sin xcos x+5cos2x+
=
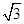 sin 2x+5×
sin 2x+5× +
+ =5sin
=5sin +5.
+5.
由 ≤x≤
≤x≤ ,得
,得 ≤2x+
≤2x+ ≤
≤ ,
,
∴- ≤sin
≤sin ≤1,∴当
≤1,∴当 ≤x≤
≤x≤ 时,函数f(x)的值域为
时,函数f(x)的值域为 .
.
(2)f(x)=5sin +5=8,
+5=8,
则sin =
= ,所以cos
,所以cos =-
=- ,
,
f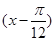 =5sin 2x+5=5sin
=5sin 2x+5=5sin +5=
+5= +7.
+7.
(3)由题意知f(x)=5sin +5→g(x)=5sin
+5→g(x)=5sin +5-5=5sin 2x,
+5-5=5sin 2x,
即g(x)=5sin 2x,
g(-x)=5sin(-2x)=-5sin 2x=-g(x),
故g(x)为奇函数.
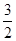
=5
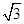 sin xcos x+2cos2x+4cos2x+sin2x+
sin xcos x+2cos2x+4cos2x+sin2x+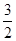 =5
=5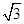 sin xcos x+5cos2x+
sin xcos x+5cos2x+
=

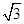 sin 2x+5×
sin 2x+5× +
+ =5sin
=5sin +5.
+5.由
 ≤x≤
≤x≤ ,得
,得 ≤2x+
≤2x+ ≤
≤ ,
,∴-
 ≤sin
≤sin ≤1,∴当
≤1,∴当 ≤x≤
≤x≤ 时,函数f(x)的值域为
时,函数f(x)的值域为 .
.(2)f(x)=5sin
 +5=8,
+5=8,则sin
 =
= ,所以cos
,所以cos =-
=- ,
,f
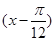 =5sin 2x+5=5sin
=5sin 2x+5=5sin +5=
+5= +7.
+7.(3)由题意知f(x)=5sin
 +5→g(x)=5sin
+5→g(x)=5sin +5-5=5sin 2x,
+5-5=5sin 2x,即g(x)=5sin 2x,
g(-x)=5sin(-2x)=-5sin 2x=-g(x),
故g(x)为奇函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
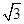 ,sinx),x∈R.
,sinx),x∈R.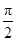 ),证明:a和b不平行;
),证明:a和b不平行;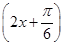 +2a+b,当x∈
+2a+b,当x∈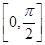 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.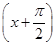 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.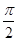 是函数f(x)=cos2
是函数f(x)=cos2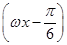 -sin2ωx(ω>0)的两个相邻的零点.
-sin2ωx(ω>0)的两个相邻的零点.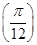 的值;
的值;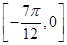 ,都有|f(x)-m|≤1,求实数m的取值范围.
,都有|f(x)-m|≤1,求实数m的取值范围.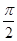 ,直线x=
,直线x=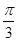 是其图象的一条对称轴,则下面各式中符合条件的解析式为 ( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为 ( )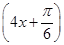
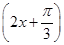 +2
+2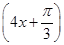 +2
+2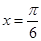 是
是 的图象的一条对称轴,则
的图象的一条对称轴,则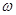 可以是( )
可以是( ) 个单位
个单位 sin
sin ,x∈R的最小正周期为________.
,x∈R的最小正周期为________.