Question

【题目】已知函数f（x）=|x-a|-1，（a为常数）．

（1）若f（x）在x∈[0，2]上的最大值为3，求实数a的值；

（2）已知g（x）=xf（x）+a-m，若存在实数a∈（-1，2]，使得函数g（x）有三个零点，求实数m的取值范围．

Answer 1

【答案】(1) a=4或-2 (2) -1＜m＜．

【解析】

（1）将写成分段函数形式,分类讨论的范围即可

（2）将有三个零点转化为和有三个不同的交点,可得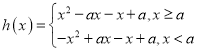,分类讨论在与时的单调性,进而由零点个数求解范围即可

解：（1）,

当时,,∴；

当时,,∴；

综上,或

（2）有三个零点,

等价于和有三个不同的交点,

,

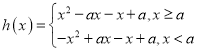当时,在上递增，在上递减,在上递增,

∴,即,

,∴

当时,在上递减,在,上递增；

∴,即,

,,∴

综上,