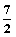题目内容
设x,y∈R+,且xy-(x+y)=1,则( )A.x+y≥
(
+1) B.xy≤
+1
C.x+y≤(
+1)2 D.xy≥
(
+1)
解析:求xy的范围,由条件xy-1=x+y≥,
即()2--1≥0.
∴(-1)2≥2.
结合xy=1+(x+y)＞1,
得≥+1.
∴xy≥(
+1)2.C,D错误.
再求x+y的范围.
由条件有x+y+1=xy≤(
)2,
即(x+y)2-4(x+y)-4≥0.
∴(x+y-2)2≥8.结合x+y≥
≥2(
+1),得x+y≥2
+2.
∴A选项正确.
答案:A
练习册系列答案
相关题目
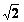+1) B.xy≤
+1
+1)2 D.xy≥2(
+1)
+1) Bx·y≤
+1
+1)2 Dx·y≥2(
+1)
B．
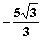C．-3
D．-