Question

（本小题共14分）

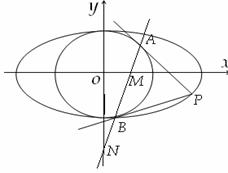
已知椭圆和圆：，过椭圆上一点引圆的两条切线，切点分别为．

（Ⅰ）（ⅰ）若圆过椭圆的两个焦点，求椭圆的离心率；

     （ⅱ）若椭圆上存在点，使得，求椭圆离心率的取值范围；

（Ⅱ）设直线与轴、轴分别交于点，，求证：为定值．

Answer 1

（共14分）

解：（Ⅰ）（ⅰ）∵ 圆过椭圆的焦点，圆：，

∴ ，

∴ ，

∴ ，

∴．                                 

（ⅱ）由及圆的性质，可得，

∴

∴

∴，．                        ---------------- 6分

（Ⅱ）设，则

整理得

 ∴方程为：，

方程为：．

∴，

∴,

直线方程为    ，即   ．

令，得，令，得，

∴，

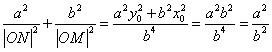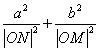∴为定值，定值是．      ----------------14分