题目内容
过点A(3,-1)作直线l交x轴于点B,交直线l1:y=2x于点C,若|BC|=2|AB|,求直线l的方程.
当k不存在时,B(3,0),C(3,6).
此时|BC|=6,|AB|=1,|BC|≠2|AB|,

∴直线l的斜率存在,
∴设直线l的方程为:y+1=k(x-3),
令y=0得B(3+ ,0),
,0),
由 得C点横坐标xc=
得C点横坐标xc= .
.
若|BC|=2|AB|则|xB-xC|=2|xA-xB|,
∴| -
- -3|=2|
-3|=2| |,
|,
∴ -
- -3=
-3= 或
或 -
- -3=-
-3=- ,
,
解得k=- 或k=
或k=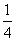 .
.
∴所求直线l的方程为:3x+2y-7=0或x-4y-7=0.

练习册系列答案
相关题目
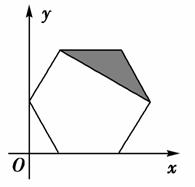
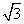 B.
B.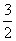
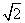 D.4
D.4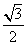
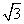 D.
D.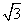 y=4相切.圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
y=4相切.圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求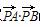 的取值范围.
的取值范围.