题目内容
14.已知a,b为非零向量,则下列命题中真命题的个数为( )①若|a|+|b|=|a+b|,则a与b方向相同;
②若|a|+|b|=|a-b|,则a与b方向相反;
③若|a|+|b|=|a-b|,则a与b有相等的模;
④若|a|-|b|=|a-b|,则a与b方向相同.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 直接利用向量共线的基本性质逐一核对四个命题得答案.
解答 解:对于①,若|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}+\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$方向相同,①正确;
对于②,若|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$方向相反,②正确;
对于③,若|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$方向相反,但$\overrightarrow{a}$与$\overrightarrow{b}$的模不一定,③错误;
对于④,若|$\overrightarrow{a}$|-|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$方向相同,④正确.
∴正确命题的个数是3个,
故选:D.
点评 本题考查命题的真假判断与应用,考查了向量共线的基本性质,是基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.执行如图所示的程序框图,如果输入的N=2016,那么输出的S=( )
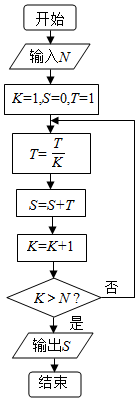

| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$ | B. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2015!}$ | ||
| C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2016}$ | D. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$ |
9.已知a=1,b,c∈{1,2,4},则以a,b,c为长度的三条线段能构成三角形的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{10}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
6.如图所示的程序框图中按程序运行后输出的结果( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |