雅礼中学教务处采用系统抽样方法.从学校高三年级全体1000名学生中抽50名学生做学习状况问卷调查．现将1000名学生从1到1000进行编号.求得间隔数k=20.即分50组每组20人．在第一组中随机抽取一个号.如果抽到的是17号.则第8组中应取的号码是( )A．177B．157C．417D．367 题目和参考答案——青夏教育精英家教网—

题目内容

4．雅礼中学教务处采用系统抽样方法，从学校高三年级全体1000名学生中抽50名学生做学习状况问卷调查．现将1000名学生从1到1000进行编号，求得间隔数k=20，即分50组每组20人．在第一组中随机抽取一个号，如果抽到的是17号，则第8组中应取的号码是（　　）

A．

177

B．

157

C．

417

D．

367

分析根据系统抽样的定义进行计算即可得到结论．

解答解：根据系统抽样的定义可知抽取的号码构成以17为首项，公差d=20的等差数列{a_n}，
∴a_n=17+20（n-1）=20n-3，
n=8，a₈=157，
故选：B．

点评本题主要考查系统抽样的应用，根据系统抽样转化为等差数列是解决本题的关键，比较基础．

练习册系列答案

高效复习计划小学毕业升学总复习系列答案

小学生10分钟口算测试100分系列答案

[$\sqrt{2}$+$\sqrt{13}$，+∞）

-a⁶

a⁶

a⁵

a⁹

12．已知集合M={x|x≤a}，N={-2，0，1}，若M∩N={-2，0}，则实数a的取值范围是[0，1）．

19．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}x，（x＞0）}\\{{2}^{x}，（x≤0）}\end{array}\right.$则f（f（$\frac{1}{3}$））=（　　）

9．在数列{a_n}中a₁=2，a₂=4，且当n≥2，n∈N^*时，a_n²=a_n-1a_n+1
（1）数列{a_n}的前n项和为S_n，证明：S_n=2a_n-2；
（2）若b_n=（2n-1）a_n，数列{b_n}的前n项和为T_n，证明：T_n+1＞4b_n．

16．

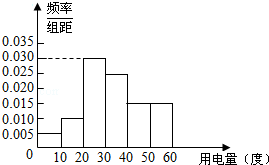某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：

分组	频数	频率
[0，10）		0.05
[10，20）		0.10
[20，30）	30
[30，40）		0.25
[40，50）		0.15
[50，60]	15
合计	n	1

（1）求月均用电量的中位数与平均数估计值；
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．

13．已知定义在[0，+∞）的函数f（x）满足f（x）=3f（x+2），当x∈[0，2）时，f（x）=-x²+2x．设f（x）在[2n-2，2n）上的最大值为${a_n}，n∈{N^*}$，则{a_n}的前n项和S_n=$\frac{3}{2}[{1-{{（{\frac{1}{3}}）}^n}}]$．

14．函数f（x）=lg（9-x²）的定义域为（-3，3），单调递增区间为（-3，0]．

试题分类