题目内容
10.己知二次函数f(x)=x2-2x-1.(1)求f(x)在[0,3]上的最大值;
(2)设f(x)在[t,t+2]上的最小值为g(t),求g(t)的最小值.
分析 (1)根据二次函数的图象和性质,可得当x=3时,函数取最大值2;
(2)分析给定区间与函数图象对称轴的关系,分类讨论,可得g(t)的最小值.
解答 解:(1)二次函数f(x)=x2-2x-1的图象是开口朝上,且以直线x=1为对称轴的抛物线,
故在[0,3]上,当x=3时,函数取最大值2;
(2)当t+2≤1,即t≤-1时,f(x)在[t,t+2]上为减函数,当x=t+2时,g(t)取最小值t2+2t-1;
当t<1<t+2时,f(x)在[t,1]上为减函数,在[1,t+2]上为增函数,当x=1时,g(t)取最小值-2;
当t≥1时,f(x)在[t,t+2]上为增函数,当x=t时,g(t)取最小值t2-2t-1;
综上所述,g(t)的最小值为$\left\{\begin{array}{l}{t}^{2}+2t-1,t≤-1\\-2,-1<t<1\\{t}^{2}-2t-1,t≥1\end{array}\right.$
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
2.已知a,b,c为△ABC的三个内角A,B,C的对边,向量$\overrightarrow{m}$=($\sqrt{3}$,-1),$\overrightarrow{n}$=(cosA,sinA),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则角A的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
20.函数f(x)=x2+(a-3)x+1在区间[-1,+∞)上是递增的,则实数a的取值范围是( )
| A. | [-3,0) | B. | (-∞,-3] | C. | [5,+∞) | D. | (0,5] |
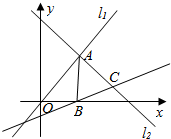 在平面直角坐标系xOy中,设直线l1:kx-y=0,直线l2:(2k-1)x+(k-1)y-7k+4=0.
在平面直角坐标系xOy中,设直线l1:kx-y=0,直线l2:(2k-1)x+(k-1)y-7k+4=0.