题目内容
已知p：“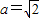
”，q：“直线x+y=0与圆x2+（y-a）2=1相切”，则p是q的（ ）A．充分非必要条件
B．必要非充分条件
C．充要条件
D．既非充分也非必要条件
【答案】分析：当a等于
时，把a的值代入圆的方程中，找出圆心坐标和圆的半径，根据点到直线的距离公式求出圆心到直线x+y=0的距离d，发现d等于圆的半径r，进而得到直线与圆的位置关系是相切；而当直线x+y=0与圆相切时，由圆心坐标和圆的半径，利用点到直线的距离公式表示出圆心（0，a）到直线x+y=0的距离d，让d等于圆的半径1列出关于a的方程，求出方程的解即可得到a的值为两个值，综上，得到p是q的充分非必要条件．
解答：解：当a=
时，圆的方程为：x2+（y-
）2=1，
则圆心坐标为（0，
），半径r=1，
所以圆心到直线x+y=0的距离d=
=1=r，
则直线与圆的位置关系是相切；
而当直线与圆的位置关系相切时，圆心坐标为（0，a），半径r=1，
则圆心到直线AB的距离d=
=1，解得a=±
，
所以p是q的充分非必要条件．
故选A
点评：此题考查学生掌握直线与圆相切时满足的条件，灵活运用点到直线的距离公式化简求值，掌握必要、充分及充要条件的判断方法，是一道中档题．
时，把a的值代入圆的方程中，找出圆心坐标和圆的半径，根据点到直线的距离公式求出圆心到直线x+y=0的距离d，发现d等于圆的半径r，进而得到直线与圆的位置关系是相切；而当直线x+y=0与圆相切时，由圆心坐标和圆的半径，利用点到直线的距离公式表示出圆心（0，a）到直线x+y=0的距离d，让d等于圆的半径1列出关于a的方程，求出方程的解即可得到a的值为两个值，综上，得到p是q的充分非必要条件．解答：解：当a=
时，圆的方程为：x2+（y-）2=1，则圆心坐标为（0，
），半径r=1，所以圆心到直线x+y=0的距离d=
=1=r，则直线与圆的位置关系是相切；
而当直线与圆的位置关系相切时，圆心坐标为（0，a），半径r=1，
则圆心到直线AB的距离d=
=1，解得a=±，所以p是q的充分非必要条件．
故选A
点评：此题考查学生掌握直线与圆相切时满足的条件，灵活运用点到直线的距离公式化简求值，掌握必要、充分及充要条件的判断方法，是一道中档题．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
已知P=2-
，Q=（
）3，R=（
）3，则P，Q，R的大小关系是 ）
| 3 |
| 2 |
| 2 |
| 5 |
| 1 |
| 2 |
| A、P＜Q＜R |
| B、Q＜R＜P |
| C、Q＜P＜R |
| D、R＜Q＜P |
已知p：Φ
{0}，q：{2}∈{1，2，3}由他们构成的新命题：“﹁p”，“﹁q”，“p∧q”，“p∨q”中，真命题有（ ）
|
| A、1个 | B、2个 | C、3个 | D、4个 |