题目内容
16. 利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=25内的个数为( )
利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=25内的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由程序框图知,得出打印的点坐标,判定该点是否在圆内即可.
解答 解:由程序框图知,
i=6时,打印第一个点(-3,6),在圆x2+y2=25外,
i=5时,打印第二个点(-2,5),在圆x2+y2=25外,
i=4时,打印第三个点(-1,4),在圆x2+y2=25内,
i=3时,打印第四个点(0,3),在圆x2+y2=25内,
i=2时,打印第五个点(1,2),在圆x2+y2=25内,
i=1时,打印第六个点(2,1),在圆x2+y2=25内,
∴打印的点在圆x2+y2=25内有4个.
故选:C.
点评 本题主要考查了循环结构,当满足条件,执行循环,不满足条件算法结束,是基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
4.已知f(x)为定义在$(0,\frac{π}{2})$上的函数,f'(x)是它的导函数,且$\frac{f'(x)}{tanx}<f(x)$恒成立,则( )
| A. | $f(\frac{π}{3})<\sqrt{3}f(\frac{π}{6})$ | B. | $f(\frac{π}{6})<\sqrt{2}f(\frac{π}{4})$ | C. | $f(\frac{π}{3})<f(\frac{π}{4})$ | D. | $f(\frac{π}{4})<\sqrt{3}f(\frac{π}{3})$ |
1.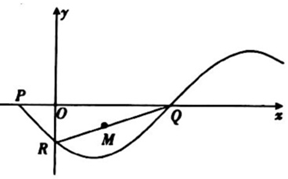 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )| A. | 1 | B. | -1 | C. | $\frac{\sqrt{6}}{2}$ | D. | -$\frac{\sqrt{6}}{2}$ |
8.等差数列{an}中,a7=4,a8=1,则a10=( )
| A. | -5 | B. | -2 | C. | 7 | D. | 10 |
5.若对于任意实数m∈[0,1],总存在唯一实数x∈[-1,1],使得m+x2ex-a=0成立,则实数a的取值范围是( )
| A. | [1,e] | B. | $({1+\frac{1}{e},e}]$ | C. | (0,e] | D. | $[{1+\frac{1}{e},e}]$ |
6.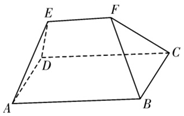 中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
 中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )
中国古代数学家名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形ABCD为正方形,四边形ABFE、CDEF为两个全等的等腰梯形,AB=4,EF$\underset{∥}{=}$$\frac{1}{2}$AB,若这个刍甍的体积为$\frac{40}{3}$,则异面直线AB与CF所成角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
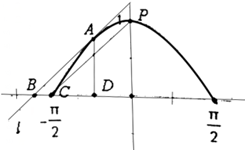 直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.
直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.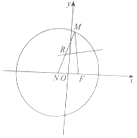 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.