题目内容
7.过点(1,1)的直线l与圆(x-2)2+(y-3)2=9相交于A,B两点,当|AB|=4时,直线l的方程为x+2y-3=0.分析 当直线l的斜率不存在时,直线l的方程为:x=1,不符合题意;当直线l的斜率存在时,圆心到直线kx-y-k+1=0的距离d=$\frac{|k-2|}{\sqrt{{k}^{2}+1}}$=$\sqrt{5}$,解得k=-$\frac{1}{2}$,由此能求出直线l的方程.
解答 解:直线l:经过点(1,1)与圆(x-2)2+(y-3)2=9相交于A,B两点,|AB|=4,则圆心到直线的距离为$\sqrt{5}$,
当直线l的斜率不存在时,直线l的方程为:x=1,不符合题意;
当直线l的斜率存在时,设直线l:y=k(x-1)+1,即kx-y-k+1=0
圆心到直线kx-y-k+1=0的距离d=$\frac{|k-2|}{\sqrt{{k}^{2}+1}}$=$\sqrt{5}$,解得k=-$\frac{1}{2}$,
∴直线l的方程为x+2y-3=0.
故答案为:x+2y-3=0.
点评 本题考查直线方程的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
17.若$α,β∈[-\frac{π}{2},\frac{π}{2}]$,且αsinα-βsinβ>0,则下列关系式:①α>β;②α<β;③α+β>0;④α2>β2;⑤α2≤β2其中正确的序号是:④.
15.某公司有A、B、C、D四辆汽车,其中A车的车牌尾号为8,B、C两辆车的车牌尾号为2,D车的车牌尾号为3,已知在非限行日,每辆车都有可能出车或不出车.已知A、D两辆汽车每天出车的概率为$\frac{2}{3}$,B、C两辆汽车每天出车的概率为$\frac{1}{2}$,且四辆汽车是否出车是相互独立的.
该公司所在地区汽车限行规定如下:
(I)求该公司在星期二至少有2辆汽车出车的概率;
(Ⅱ)设ξ表示该公司在星期三和星期四两天出车的车辆数之和,求ξ的分布列和数学期望.
该公司所在地区汽车限行规定如下:
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(Ⅱ)设ξ表示该公司在星期三和星期四两天出车的车辆数之和,求ξ的分布列和数学期望.
16. 利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=25内的个数为( )
利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=25内的个数为( )
 利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=25内的个数为( )
利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x2+y2=25内的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
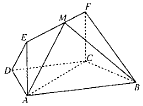 如图,在四边形ABCD中,AB∥CD,∠BCD=$\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF.
如图,在四边形ABCD中,AB∥CD,∠BCD=$\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF.