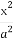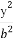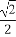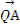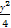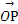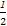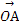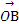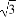Question

已知椭圆E: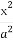+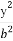=1(a>b>0)的离心率e=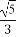,a2与b2的等差中项为.

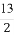(1)求椭圆E的方程.

(2)A,B是椭圆E上的两点,线段AB的垂直平分线与x轴相交于点P(t,0),求实数t的取值范围.

 

Answer 1

(1) +=1 (2) (-,)

【解析】(1)由题意得

解得:.即椭圆E的方程为+=1.

(2)设A,B的坐标分别为(x1,y1),(x2,y2).

因线段AB的垂直平分线与x轴相交,

故AB不平行于y轴,即x1≠x2.

又交点为P(t,0),故|PA|=|PB|,

即(x1-t)2+=(x2-t)2+,

∴t=+　①

∵A,B在椭圆上,∴=4-,=4-.

将上式代入①,得t=.

又∵-3≤x1≤3,-3≤x2≤3,且x1≠x2,

∴-6<x1+x2<6,则-<t<,

即实数t的取值范围是(-,).