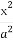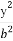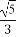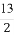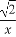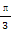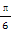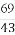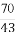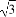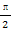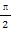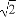Question

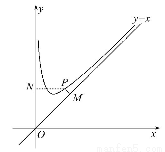
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为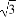米(将眼睛S距地面的距离SA按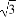米处理).

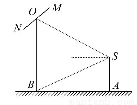
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.

(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.

 

Answer 1

(1) AB为3米 OB为2米 (2) 当视角∠MSN取最大值时,cosθ=.

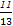【解析】(1)如图,作SC⊥OB于C,

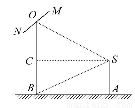
依题意∠CSB=30°,∠ASB=60°.

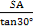又SA=,故在Rt△SAB中,可求得AB==3,

即摄影爱好者到立柱的水平距离AB为3米.

在Rt△SCO中,SC=3,∠CSO=30°,OC=SC·tan 30°=,

又BC=SA=,故OB=2,即立柱的高度OB为2米.

(2)方法一:如图,以O为原点,以水平方向向右为x轴正方向建立平面直角坐标系,连接SM,SN,

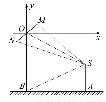
设M(cosα,sinα),α∈[0,2π),

则N(-cosα,-sinα),由(1)知S(3,-).

故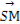=(cosα-3,sinα+),

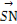=(-cosα-3,-sinα+),

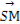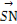∵·=(cosα-3)·(-cosα-3)+(sinα+)·(-sinα+)=11.

||·||=·

=·

=

=.

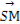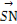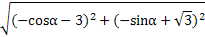
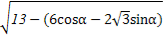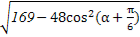由α∈[0,2π)知|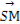|·||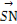∈[11,13].

所以cos∠MSN=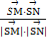∈[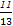,1],易知∠MSN为锐角,

故当视角∠MSN取最大值时,cosθ=.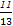

方法二:∵cos∠MOS=-cos∠NOS,

∴=-

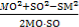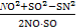
于是得SM2+SN2=26从而

cosθ=≥=.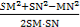

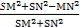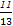又∠MSN为锐角,

故当视角∠MSN取最大值时,cosθ=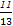.