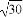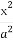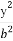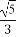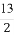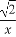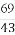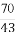Question

过点Q(-2,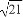)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.

(1)求r的值.

(2)设P是圆O上位于第一象限内的任意一点,过点P作圆O的切线l,且l交x轴于点A,交y轴于点B,设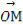=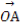+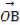,求|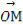|的最小值(O为坐标原点).

 

Answer 1

(1)3 (2)6

【解析】(1)圆O:x2+y2=r2(r>0)的圆心为O(0,0),于是|QO|2=(-2)2+()2=25,

由题设知,△QDO是以D为直角顶点的直角三角形,

故有r=|OD|===3.

(2)设直线l的方程为+=1(a>0,b>0),

即bx+ay-ab=0,则A(a,0),B(0,b),

∴=(a,b),∴||=.

∵直线l与圆O相切,

∴=3⇒a2b2=9(a2+b2)≤()2,

∴a2+b2≥36,∴||≥6,

当且仅当a=b=3时取到“=”.

∴||取得最小值为6.