题目内容
已知tan(α+β)=
,tan(β-
)=
,则sin(α+
)sin(
-α)的值为 .
| 2 |
| 5 |
| π |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| π |
| 4 |
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:首先,根据已知条件,得到tan(α+
)=tan[(α+β)-(β-
)]=
,然后,求解得到tanα=-
,然后,再结合sin(α+
)sin(
-α)=
sin[2(α+
)]=
cos2α=
×
=
×
=
.从而得到结果.
| π |
| 4 |
| π |
| 4 |
| 3 |
| 22 |
| 19 |
| 25 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1-tan2α |
| 1+tan2α |
| 1 |
| 2 |
1-(-
| ||
1+(-
|
| 66 |
| 493 |
解答:
解:∵tan(α+β)=
,tan(β-
)=
,
∴tan(α+
)=tan[(α+β)-(β-
)]
=
=
=
,
∴
=
,
∴tanα=-
,
∵sin(α+
)sin(
-α)
=
sin[2(α+
)]
=
cos2α
=
×
=
×
=
.
故答案为:
.
| 2 |
| 5 |
| π |
| 4 |
| 1 |
| 4 |
∴tan(α+
| π |
| 4 |
| π |
| 4 |
=
tan(α+β)-tan(β-
| ||
1+tan(α+β)tan(β-
|
=
| ||||
1+
|
=
| 3 |
| 22 |
∴
| 1+tanα |
| 1-tanα |
| 3 |
| 22 |
∴tanα=-
| 19 |
| 25 |
∵sin(α+
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| π |
| 4 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1-tan2α |
| 1+tan2α |
=
| 1 |
| 2 |
1-(-
| ||
1+(-
|
=
| 66 |
| 493 |
故答案为:
| 66 |
| 493 |
点评:本题重点考查了二倍角公式、两角和与差的公式等知识,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 如图是函数y=Asin(ωx+φ)x∈R在区间[-
如图是函数y=Asin(ωx+φ)x∈R在区间[-| π |
| 6 |
| 5π |
| 6 |
| π |
| 2 |
A、向左平移
| ||||
B、向左平移
| ||||
C、向左平移
| ||||
D、向左平移
|
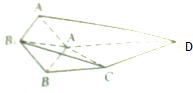 如图,ABCD为直角梯形,AB⊥AD,四边形ABB1A1是平行四边形,侧面ADA1⊥底面ABCD,AA1=
如图,ABCD为直角梯形,AB⊥AD,四边形ABB1A1是平行四边形,侧面ADA1⊥底面ABCD,AA1= 如图,在直角坐标系xOy中,锐角△ABC内接于单位圆,已知BC平行于x轴,且tan∠xDA=2,记∠xOA=α(0<α<
如图,在直角坐标系xOy中,锐角△ABC内接于单位圆,已知BC平行于x轴,且tan∠xDA=2,记∠xOA=α(0<α<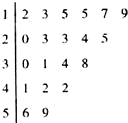 为了解某校教师使用多媒体辅助教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了解他们上学期使用多媒体辅助教学的次数,结果用茎叶图表示(如图),据此可估计该校上学期200名教师中,使用多媒体辅助教学不少于30次的教师人数为
为了解某校教师使用多媒体辅助教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了解他们上学期使用多媒体辅助教学的次数,结果用茎叶图表示(如图),据此可估计该校上学期200名教师中,使用多媒体辅助教学不少于30次的教师人数为