Question

【题目】已知圆和椭圆， 是椭圆的左焦点．

（Ⅰ）求椭圆的离心率和点的坐标；

（Ⅱ）点在椭圆上，过作轴的垂线，交圆于点（不重合），是过点的圆的切线．圆的圆心为点，半径长为．试判断直线与圆的位置关系，并证明你的结论．

Answer 1

【答案】（Ⅰ）见解析;（Ⅱ）见解析．

【解析】试题分析：（Ⅰ）由椭圆的标准方程为，可得，所以椭圆的离心率，椭圆的左焦点的坐标为；（Ⅱ） 设，其中，则，可设，则，由点斜式可得直线的方程为，圆的圆心到直线的距离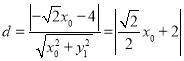．利用两点间距离公式求得，即 ，从而可得直线与圆相切．

试题解析：（Ⅰ）由题意，椭圆的标准方程为．

所以， ，从而．

因此， ．

故椭圆的离心率．

椭圆的左焦点的坐标为．

（Ⅱ）直线与圆相切．证明如下：

设，其中，则，

依题意可设，则．

直线的方程为，

整理为 ．

所以圆的圆心到直线的距离．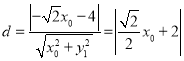

因为．

所以，

即 ，

所以 直线与圆相切．