题目内容
7．
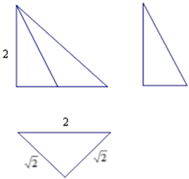一个几何体的三视图如图．该几何体的各个顶点都在球O的球面上，球O的体积为（ ）| A． | $\frac{\sqrt{2}}{3}$π | B． | $\frac{4\sqrt{2}}{3}$π | C． | $\frac{8\sqrt{2}}{3}$π | D． | $\frac{10\sqrt{2}}{3}$π |
分析 几何体为三棱锥，且三棱锥的一条侧棱与底面垂直，底面为等腰直角三角形，取O为SC的中点，可证OS=OC=OA=OB，由此求得外接球的半径，代入球的体积公式计算．
解答 
解：由三视图知：几何体为三棱锥，且三棱锥的一条侧棱与底面垂直，高为2，
底面为等腰直角三角形，如图：SA⊥平面ABC，SA=2，AC的中点为D，
在等腰直角三角形SAC中，取O为SC的中点，∴OS=OC=OA=OB，
∴O为三棱锥外接球的球心，R=$\sqrt{2}$，
∴外接球的体积V=$\frac{4}{3}$π×（$\sqrt{2}$）3=$\frac{8\sqrt{2}}{3}$．
故选：C．
点评 本题考查了由三视图求几何体的外接球的体积，判断几何体的特征性质及数据所对应的几何量是关键．
练习册系列答案
相关题目
如图，已知点A、B的坐标分别是（-3，0），（3，0），点C为线段AB上任一点，P、Q分别以AC和BC为直径的两圆O1，O2的外公切线的切点，求线段PQ的中点的轨迹方程．