题目内容
16.已知sinα=$\frac{4}{5}$,且$\frac{π}{2}<α<π$,求sin(α+$\frac{π}{4}$)、cos(α+$\frac{π}{4}$)、tan(α+$\frac{π}{4}$).分析 利用同角三角函数关系,再利用两角和与差的正弦、余弦以及正切函数进行解答.
解答 解:∵sinα=$\frac{4}{5}$,且$\frac{π}{2}<α<π$,
∴cosα=-$\sqrt{1-(\frac{4}{5})^{2}}$=-$\frac{3}{5}$,
∴sin(α+$\frac{π}{4}$)=sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$=$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$-$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{10}$.
cos(α+$\frac{π}{4}$)=cosαcos$\frac{π}{4}$-sinαsin$\frac{π}{4}$=-$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$-$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$=-$\frac{7\sqrt{2}}{10}$.
tan(α+$\frac{π}{4}$)=$\frac{sin(α+\frac{π}{4})}{cos(α+\frac{π}{4})}$=$\frac{\frac{\sqrt{2}}{10}}{-\frac{7\sqrt{2}}{10}}$=-$\frac{1}{7}$.
点评 本题考查同角三角函数关系,两角和与差的正弦、余弦以及正切函数,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.若圆M在x轴与y轴上截得的弦长总相等,则圆心M的轨迹方程是( )
| A. | x-y=0 | B. | x+y=0 | C. | x2+y2=0 | D. | x2-y2=0 |
7.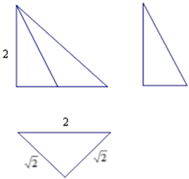 一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
 一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )| A. | $\frac{\sqrt{2}}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | $\frac{10\sqrt{2}}{3}$π |
11. 一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
 一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 6 | D. | $\frac{20}{3}$ |