题目内容
若f(x)=4sinωx(0<ω<1)在区间[0,
]上的最大值为2
,则函数g(x)=tan[π(ωx-
)]的最小正周期为( )
| π |
| 3 |
| 2 |
| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据题意可推断出sinωx在此区间上的最大值,利用x的范围确定ωx的范围,进而可推断出x=
时函数有最大值,进而求得ω的值,然后利用三角函数的周期公式求得函数g(x)的最小正周期.
| π |
| 3 |
解答:解;依题意可知函数在区间[0,
]上的最大值2
,
则函数sinωx在此区间上的最大值为
,
∵0≤x≤
∴0≤ωx≤
ω•
=
ω=
∴g(x)=tan[π(ωx-
)]的最小正周期为T=
=
,
故选B.
| π |
| 3 |
| 2 |
则函数sinωx在此区间上的最大值为
| ||
| 2 |
∵0≤x≤
| π |
| 3 |
∴0≤ωx≤
| π |
| 4 |
ω•
| π |
| 3 |
| π |
| 4 |
ω=
| 3 |
| 4 |
∴g(x)=tan[π(ωx-
| 1 |
| 6 |
| π | ||
π•
|
| 4 |
| 3 |
故选B.
点评:本题主要考查了三角函数的周期性及其求法.考查了学生的分析问题和推理的能力.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
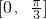 上的最大值为
上的最大值为 ,则函数
,则函数 的最小正周期为
的最小正周期为



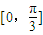 上的最大值为
上的最大值为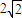 ,则函数
,则函数 的最小正周期为( )
的最小正周期为( )


