题目内容

函数f(x)=Asin(ωx+φ)+k(A＞0，ω＞0，|φ|＜
π
2
)的图象如图所示，则f（x）的表达式是f（x）=
3
2
sin(2x+
π
3
)+1
3
2
sin(2x+
π
3
)+1
．
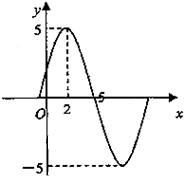
分析：由函数图象知，函数的最大值是
5
2
，最小值是-
1
2
，易求出A与K，又由最高点的横坐标与最低点的横坐标求出
T
2
，即可求出ω，再将点（
π
12
，
5
2
）代入求出φ即可得到函数的解析式
解答：解：由图知，周期T=2(
7π
12
-
π
12
)=π，所以ω=2．
又
5
2
-
1
2
2
=1，所以k=1．
因为
5
2
-1=
3
2
，则A=
3
2
．
由f(
π
12
)=
5
2
，得sin（2×
π
12
+φ）=1，即得2×
π
12
+φ=
π
2
得φ=
π
3
．
故f(x)=
3
2
sin(2x+
π
3
)+1．
故答案为
3
2
sin(2x+
π
3
)+1
点评：本题考查由f（x）=Asin（ωx+φ）+k的部分图象确定其解析式，解题的关键是从图象的几何特征得出解析式中参数的方程求出参数，求解本题难点是求初相φ的值，一般是利用最值点的坐标建立方程求之，若代入的点不是最值点，要注意其是递增区间上的点还是递减区间上的点，确定出正确的相位值，求出初相，此处易出错，要好好总结规律．
练习册系列答案
相关题目
精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）若图象g（x）与函数f（x）的图象关于点P（4，0）对称，求函数g（x）的单调递增区间．
（2013•大连一模）已知函数f(x)=Asin(ωx+φ)(x∈R，A＞0，ω＞0，|φ|＜
π
2
)的图象（部分）如图所示，则ω，φ分别为（　　）
当x∈[-
π
6
，
2π
3
]时，函数f(x)=Asin(ωx+θ) (A＞0，ω＞0，|θ|＜
π
2
)的图象如图所示．
（1）求函数f（x）在[-
π
6
，
2π
3
]上的表达式；
（2）求方程f(x)=
2
2
在[-
π
6
，
2π
3
]的解集．
精英家教网函数f(x)=Asin(ωx+φ)，x∈R(A＞0，ω＞0，|φ|＜
π
2
)的一段图象如图5所示：将y=f（x）的图象向右平移m（m＞0）个单位，可得到函数y=g（x）的图象，且图象关于原点对称，g(
π
2013
)＞0．
（1）求A、ω、φ的值；
（2）求m的最小值，并写出g（x）的表达式；
（3）若关于x的函数y=g(
tx
2
)在区间[-
π
3
，
π
4
]上最小值为-2，求实数t的取值范围．
精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，x∈R，|φ|＜
π
2
)的图象（部分）如图所示，则f（x）的解析式是（　　）
A、f(x)=5sin(
π
3
x+
π
6
)
B、f(x)=5sin(
π
6
x-
π
6
)
C、f(x)=5sin(
π
6
x+
π
6
)
D、f(x)=5sin(
π
3
x-
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网