题目内容
设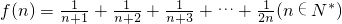 ,那么f(n)-m≥0对于n(n∈N*,n≥2)恒成立,则m的取值范围为
,那么f(n)-m≥0对于n(n∈N*,n≥2)恒成立,则m的取值范围为
- A.
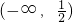
- B.
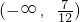
- C.
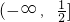
- D.
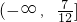
D
分析:计算f(n+1)-f(n)的值大于零,可得函数f(n)为增函数,故n≥2时,函数f(n)的最小值为f(2),结合题意可得f(2)≥m,由此求得m的取值范围.
解答:∵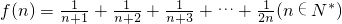 ,
,
∴f(n+1)= ,
,
∴f(n+1)-f(n)=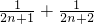 -
- =
=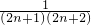 >0.
>0.
故函数f(n)为增函数,故n≥2时,函数f(n)的最小值为f(2)= +
+ =
= ,
,
再由f(n)-m≥0对于n(n∈N*,n≥2)恒成立,故有 ≥m.
≥m.
故m的取值范围为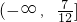 ,
,
故选D.
点评:本题主要考查利用函数的单调性求函数的最值,函数的恒成立问题,求出f(n)的最小值属于中档题.
分析:计算f(n+1)-f(n)的值大于零,可得函数f(n)为增函数,故n≥2时,函数f(n)的最小值为f(2),结合题意可得f(2)≥m,由此求得m的取值范围.
解答:∵
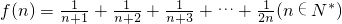 ,
,∴f(n+1)=
 ,
,∴f(n+1)-f(n)=
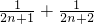 -
- =
=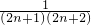 >0.
>0.故函数f(n)为增函数,故n≥2时,函数f(n)的最小值为f(2)=
 +
+ =
= ,
,再由f(n)-m≥0对于n(n∈N*,n≥2)恒成立,故有
 ≥m.
≥m.故m的取值范围为
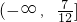 ,
,故选D.
点评:本题主要考查利用函数的单调性求函数的最值,函数的恒成立问题,求出f(n)的最小值属于中档题.

练习册系列答案
相关题目
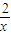 ,x∈(
,x∈( ,2),那么m+n的值( )
,2),那么m+n的值( )