题目内容
如果对于函数y=f(x)的定义域内的任意x,都有N≤f(x)≤M(M,N为常数)成立,那么称f(x)为可界定函数,M为上界值,N为下界值.设上界值中的最小值为m,下界值中的最大值为n.给出函数f(x)=2x+
,x∈(
,2),那么m+n的值( )
| 2 |
| x |
| 1 |
| 2 |
| A、大于9 | B、等于9 |
| C、小于9 | D、不存在 |
分析:根据如果对于函数y=f(x)的定义域内的任意x,都有N≤f(x)≤M(M,N为常数)成立,那么称f(x)为可界定函数,M为上界值,N为下界值.设上界值中的最小值为m,下界值中的最大值为n.对于函数f(x)=2x+
,x∈(
,2),求其上界值中的最小值为m,下界值中的最大值为n,实质就是求函数f(x)=2x+
在[
,2]上的最值.
| 2 |
| x |
| 1 |
| 2 |
| 2 |
| x |
| 1 |
| 2 |
解答:解:f(x)=2x+
,x∈(
,2),
f(x)=2x+
≥2
=4,当且仅当x=1时,等号成立,
∴f(X)min=4,f(x)max=max{f(
),f(2)}<5
∴m=5,n=4,∴m+n=9.
故选B.
| 2 |
| x |
| 1 |
| 2 |
f(x)=2x+
| 2 |
| x |
| 4 |
∴f(X)min=4,f(x)max=max{f(
| 1 |
| 2 |
∴m=5,n=4,∴m+n=9.
故选B.
点评:考查对新定义的理解和应用,转化为求函数的最值问题,体现了转化的思想,属基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
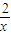 ,x∈(
,x∈( ,2),那么m+n的值( )
,2),那么m+n的值( )