题目内容
6.已知直线y=3-x与两坐标轴围成的区域为Ω1,不等式组$\left\{\begin{array}{l}{x+y≤3}\\{x≥0}\\{2x-y≤0}\end{array}\right.$所形成的区域为Ω2,在区域Ω1中随机放置一点,则该点落在区域Ω2的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由题意画出图形,分别求出区域Ω1,Ω2的面积,利用几何概型得答案.
解答 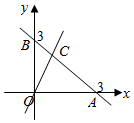 解:如图所示,△OAB对应的区域为Ω1,△OBC对应的区域为Ω2,
解:如图所示,△OAB对应的区域为Ω1,△OBC对应的区域为Ω2,
联立$\left\{\begin{array}{l}{2x-y=0}\\{x+y=3}\end{array}\right.$,解得C(1,2),
∴S△OBC=$\frac{1}{2}$×3×1=$\frac{3}{2}$,
S△OAB=$\frac{1}{2}$×3×3=$\frac{9}{2}$,
由几何概型可知,该点落在区域Ω2的概率为:
P=$\frac{{S}_{△OBC}}{{S}_{△OAB}}$=$\frac{1}{3}$.
故选:B.
点评 本题考查了简单的线性规划问题,也考查了几何概型的概率计算问题,是中档题.

练习册系列答案
相关题目
17.袋中有大小形状都相同的4个黑球和2个白球.如果不放回地依次取出2球,那么在第1次取到的是黑球的条件下,第2次取到黑球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
5.已知随机变量X~N(2,σ2),且P(1<X≤3)=0.9544,则P(2<X≤2.5)=( )
(附:随机变景X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544)
(附:随机变景X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544)
| A. | 0.9544 | B. | 0.6829 | C. | 0.4772 | D. | 0.3413 |
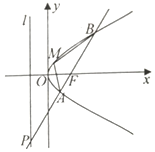 如图,F为抛物线y2=2px(p>0)的焦点,经过F点作倾斜角为锐角的直线l,与准线及抛物线的交点自下至上依次为P,A,B,且$\overrightarrow{PA}$=2$\overrightarrow{AF}$.
如图,F为抛物线y2=2px(p>0)的焦点,经过F点作倾斜角为锐角的直线l,与准线及抛物线的交点自下至上依次为P,A,B,且$\overrightarrow{PA}$=2$\overrightarrow{AF}$. 某公司为了解用户对其产品的满意度,随机调查了一些用户,得到了满意度评分的茎叶图,则这组评分数据的中位数是81.
某公司为了解用户对其产品的满意度,随机调查了一些用户,得到了满意度评分的茎叶图,则这组评分数据的中位数是81.