题目内容
16.已知△ABC中,AB=AC=4,BC=4$\sqrt{3}$,已知蚂蚁在△ABC的内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离△ABC的三个顶点距离均超过1的概率为1-$\frac{\sqrt{3}π}{24}$.分析 分别求出对应事件所表示的面积,利用几何概型的概率公式计算即可.
解答 解:∵三角形的三边长分别是4,4,4$\sqrt{3}$,
∴三角形的高AD=2,
则△ABC的面积为S=$\frac{1}{2}$×4$\sqrt{3}$×2=4$\sqrt{3}$;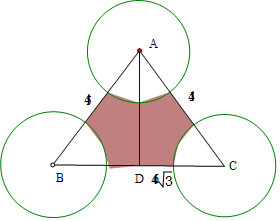
则该蚂蚁距离三角形的三个顶点的距离均超过1,对应的区域为图中阴影部分,
三个小扇形的面积之和为一个整圆的面积的$\frac{1}{2}$,圆的半径为1,
则阴影部分的面积为S1=4$\sqrt{3}$-$\frac{1}{2}$π•12=4$\sqrt{3}$-$\frac{1}{2}$π,
根据几何概型的概率公式得所求概率为
P=$\frac{4\sqrt{3}-\frac{1}{2}π}{4\sqrt{3}}$=1-$\frac{\sqrt{3}π}{24}$.
故答案为:1-$\frac{\sqrt{3}π}{24}$.
点评 本题考查了几何概型的概率计算问题,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,若t∈[0,1],则|t($\overrightarrow{b}$-$\overrightarrow{a}$)+$\overrightarrow{a}$|+|$\frac{5}{12}$$\overrightarrow{b}$+(1-t)($\overrightarrow{a}$-$\overrightarrow{b}$)|的最小值为( )
| A. | $\frac{{\sqrt{193}}}{12}$ | B. | $\frac{13}{12}$ | C. | $\sqrt{2}$ | D. | 1 |
4.函数y=$\frac{{x}^{2}+2x+2}{x+1}$(x>-1)的图象最低点的坐标是( )
| A. | (1,2) | B. | (0,2) | C. | (1,1) | D. | (1,-2) |
8.复数z=i(2+i)的共扼复数对应的点所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.已知直线y=3-x与两坐标轴围成的区域为Ω1,不等式组$\left\{\begin{array}{l}{x+y≤3}\\{x≥0}\\{2x-y≤0}\end{array}\right.$所形成的区域为Ω2,在区域Ω1中随机放置一点,则该点落在区域Ω2的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |