题目内容
10.已知函数f(x)=x2log4a,如果方程f(x-1)+2x=0无实根,则实数a的取值范围是(2,+∞).分析 化简可知(x-1)2log4a+2x=0没有实根,从而分类讨论,转化为y=(x-1)2与y=-$\frac{2}{lo{g}_{4}a}$x的图象没有交点,从而利用数形结合的方法求解.
解答 解:∵f(x)=x2log4a,
∴方程f(x-1)+2x=0可化为(x-1)2log4a+2x=0,
①若log4a=0,即a=1时,方程有实根x=0;
②若log4a≠0,则可化为(x-1)2=-$\frac{2}{lo{g}_{4}a}$x,
故只需使y=(x-1)2与y=-$\frac{2}{lo{g}_{4}a}$x的图象没有交点,
作y=(x-1)2与y=-$\frac{2}{lo{g}_{4}a}$x的图象如下,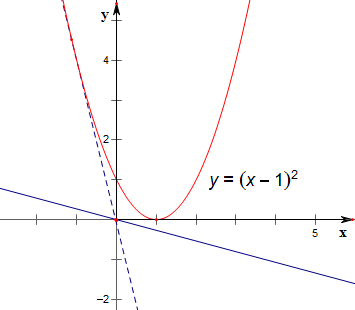
当直线与y=(x-1)2相切时,设切点为(x,(x-1)2),则
2(x-1)=$\frac{(x-1)^{2}}{x}$,解得,x=1或x=-1;
当x=-1时,2(x-1)=-4,当x=1时,2(x-1)=0;
故-4<-$\frac{2}{lo{g}_{4}a}$<0,
故log4a$>\frac{1}{2}$,
故a>2.
综上所述,a>2.
故答案为:(2,+∞).
点评 本题考查了方程的解与函数的零点的关系应用及导数的综合应用.

练习册系列答案
相关题目
20.函数y=-($\frac{1}{2}$)x的图象( )
| A. | 与函数y=($\frac{1}{2}$)x的图象关于y对称 | |
| B. | 与函数y=($\frac{1}{2}$)x的图象关于坐标原点对称 | |
| C. | 与函数y=($\frac{1}{2}$)-x的图象关于y轴对称 | |
| D. | 与函数y=($\frac{1}{2}$)-x的图象关于坐标原点对称 |
18.已知△ABC中,BC边上的高与BC边的长相等,则$\frac{A{B}^{2}+A{C}^{2}+B{C}^{2}}{AB•AC}$的最大值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |