题目内容
【题目】
已知函数
为自然对数的底数）
（1）求
的单调区间，若
有最值，请求出最值；
（2）是否存在正常数
，使
的图象有且只有一个公共点，且在该公共点处有共同的切线？若存在，求出的值，以及公共点坐标和公切线方程；若不存在，请说明理由.
【答案】(Ⅰ)所以当
时，
的单调递减区间为
，单调递增区间为
，最小值为
，无最大值 ；
(Ⅱ)存在
，使
的图象有且只有一个公共点，且在该公共点处有共同的切线，易求得公共点坐标为
，公切线方程为
．
【解析】
解：（1）
……61分
①当
恒成立
上是增函数，F只有一个单调递增区间（0，-∞），没有最值…3分
②当时，
，
若
，则
上单调递减；
若
，则
上单调递增，
时，有极小值，也是最小值，
即
…………6分
所以当时，的单调递减区间为
单调递增区间为，最小值为，无最大值…………7分
（2）方法一，若
与
的图象有且只有一个公共点，
则方程
有且只有一解，所以函数有且只有一个零点…………8分
由（1）的结论可知
…………10分
此时，
的图象的唯一公共点坐标为
又
的图象在点处有共同的切线，
其方程为
，即…………13分
综上所述，存在
，使的图象有且只有一个公共点，且在该点处的公切线方程为
…………14分
方法二：设图象的公共点坐标为
，
根据题意得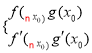
高考资源网 |
即
由②得
，代入①得
从而…………10分
此时由（1）可知
时，
因此除
外，再没有其它
，使
…………13分
故存在，使的图象有且只有一个公共点，且在该公共点处有共同的切线，易求得公共点坐标为，公切线方程为…………14分
练习册系列答案
相关题目
