题目内容
(本小题满分14分)设函数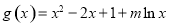 (
(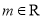 ).
).
(1)当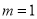 时,求过点
时,求过点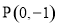 且与曲线
且与曲线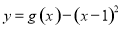 相切的切线方程;
相切的切线方程;
(2)求函数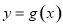 的单调递增区间;
的单调递增区间;
(3)若函数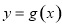 有两个极值点
有两个极值点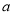 ,
,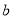 ,且
,且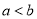 ,记
,记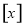 表示不大于
表示不大于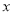 的最大整数,试比较
的最大整数,试比较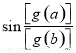 与
与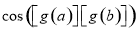 的大小.
的大小.
(1)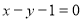 (2)
(2)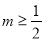 函数的增区间为
函数的增区间为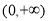 ;
;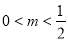 ,函数的单调增区间为
,函数的单调增区间为 与
与 ;
;  函数的单调增区间为
函数的单调增区间为
(3) 当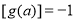 时,
时,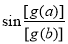
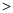
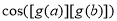 ;
;
当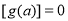 时,
时,
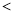
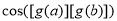
【解析】
试题分析: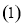 当
当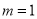 时,曲线方程为
时,曲线方程为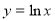 ,设切点为
,设切点为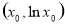 求导得到切线的斜率为
求导得到切线的斜率为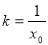
可得切线方程为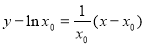 将切线过点
将切线过点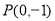 代入可得
代入可得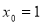 ,则切线方程易得
,则切线方程易得
(2)函数的定义域为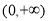 ,且
,且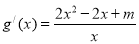 令
令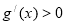 并结合定义域可得
并结合定义域可得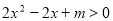 分
分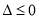 ,
,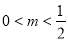 ,
, 讨论其单调增区间
讨论其单调增区间
(3)根据题意,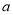 ,
,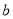 是
是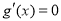 的两个根,由
的两个根,由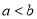 及
及 可得
可得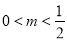 ,进而解得
,进而解得
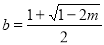 ,则
,则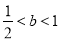 ,又由
,又由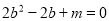 得到
得到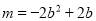 ,则
,则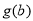 ,
,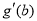 均可由
均可由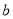 表示,且
表示,且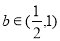 时,
时, 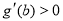 ,即函数
,即函数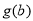 是
是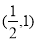 上的增函数
上的增函数
所以 ,故
,故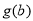 的取值范围是
的取值范围是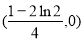
则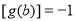 . 同理可得
. 同理可得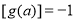 或
或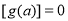 ,则
,则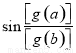 与
与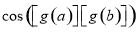 的大小可知
的大小可知
试题解析:(1)显然曲线方程为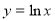 ,设切点为
,设切点为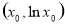
由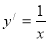 得到切线的斜率为
得到切线的斜率为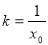 .则切线方程为
.则切线方程为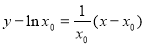
因为切线过点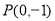 ,所以
,所以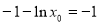 ,解得
,解得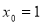
所以切线方程为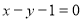
(2)显然函数的定义域为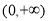 ,且
,且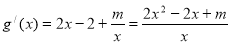
令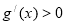 并结合定义域可得
并结合定义域可得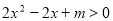
对应一元二次方程的判别式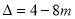
故当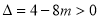 ,即
,即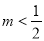 时,对应方程有两个不等实根
时,对应方程有两个不等实根
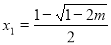 与
与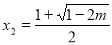
当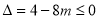 ,即
,即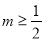 时,
时,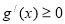 恒成立,
恒成立,
所以函数的增区间为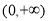
当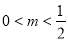 时,对应方程两根为正,故函数的单调增区间为
时,对应方程两根为正,故函数的单调增区间为
 与
与
当 时,对应方程两根
时,对应方程两根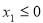 ,
,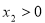 ,
,
故函数的单调增区间为
(3)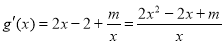 ,令
,令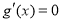 得
得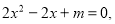
由题意知方程有两个不相等的正数根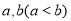 ,则
,则
解得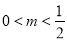 ,
,
解方程得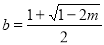 ,则
,则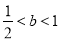 .
.
又由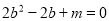 得
得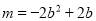 ,
,
所以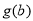 =
=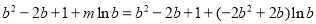 ,
,
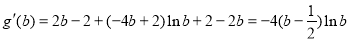
当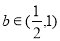 时,
时, 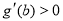 ,即函数
,即函数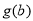 是
是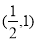 上的增函数
上的增函数
所以 ,故
,故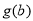 的取值范围是
的取值范围是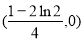
则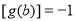 .
.
同理可求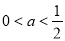 ,
,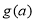 =
=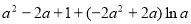 ,
,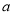

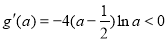 ,即函数
,即函数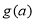 是
是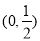 上的减函数
上的减函数
所以 ,故
,故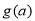 的取值范围是
的取值范围是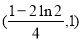
则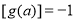 或
或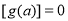
当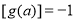 时,
时,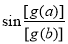
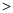
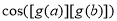 ;
;
当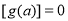 时,
时,
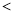
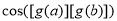 .
.
考点:利用导数研究函数的切线,单调性等性质
考点分析: 考点1:导数在研究函数中的应用 考点2:复合函数的导数 考点3:函数的单调性与导数 考点4:函数的极值与导数 考点5:函数的最值与导数 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
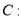
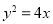 上一点
上一点 到
到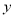 轴的距离为
轴的距离为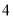 ,则点
,则点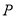 到抛物线
到抛物线 的焦点的距离是( )
的焦点的距离是( )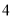 B.
B.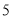 C.
C.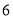 D.
D.
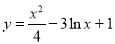 的一条切线的斜率为
的一条切线的斜率为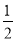 ,则切点的横坐标为( )
,则切点的横坐标为( )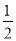
 ,
, 的夹角为
的夹角为 ,且
,且 ,
, ,则
,则
 内单调递增的函数是( )
内单调递增的函数是( ) B.
B. C.
C.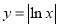 D.
D.
 .
. 的值;
的值; 的奇偶性;
的奇偶性; 为第四象限的角,且
为第四象限的角,且 ,求
,求 的值.
的值. 化为十进制数,结果为 .
化为十进制数,结果为 .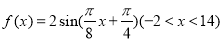 的图象与
的图象与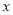 轴交于点
轴交于点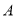 ,过点
,过点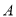 的直线
的直线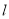 与函数
与函数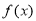 的图象交于
的图象交于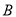 、
、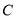 两点,
两点,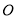 为坐标原点,则
为坐标原点,则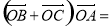 .
.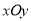 中,圆
中,圆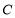 的参数方程
的参数方程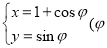 为参数).以
为参数).以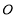 为极点,
为极点,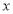 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.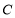 的极坐标方程;
的极坐标方程;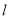 的极坐标方程是
的极坐标方程是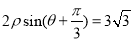 ,射线
,射线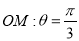 与圆
与圆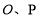 ,与直线
,与直线 的交点为
的交点为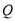 ,求线段
,求线段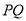 的长.
的长.