题目内容
)已知向量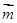 =(
=(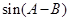 ,
,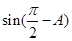 ),
),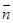 =(1,
=(1,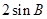 ),且
),且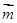
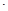
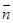 =
=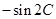 ,其中
,其中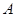 、
、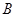 、
、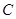 分别为
分别为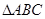 的三边
的三边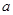 、
、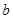 、
、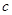 所对的角.
所对的角.
(Ⅰ)求角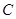 的大小;
的大小;
(Ⅱ)若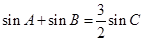 ,且
,且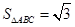 ,求边
,求边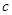 的长.
的长.
(Ⅰ);(Ⅱ) .
.
解析试题分析:(Ⅰ)由向量 ,
, ,和
,和
 ,利用数量积公式可求得
,利用数量积公式可求得 ,即
,即 ;(Ⅱ)因为
;(Ⅱ)因为 ,且
,且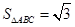 ,利用正弦定理将角转化为边,利用余弦定理来求
,利用正弦定理将角转化为边,利用余弦定理来求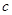
试题解析:(Ⅰ)


在 中,
中, ,
, ,所以
,所以 ,又
,又
 , 所以
, 所以 ,所以
,所以 ,即
,即 ;
;
(Ⅱ)因为 ,由正弦定理得
,由正弦定理得 ,
,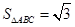 ,得
,得 ,由余弦定理得,解得
,由余弦定理得,解得 .
.
考点:1、向量的数量积, 2、三角恒等变形, 3、解三角形.

练习册系列答案
相关题目
 为偶函数,周期为2
为偶函数,周期为2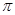 .
.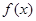 的解析式;
的解析式; 的值.
的值. 的部分图象如图所示.
的部分图象如图所示.
 的解析式;
的解析式; ,求
,求 的值.
的值. ,
, 时,求
时,求 在区间
在区间 上的取值范围;
上的取值范围;
 =2时,
=2时, =
= ,求
,求 的值。
的值。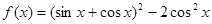
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;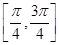 上的值域.
上的值域.
 ,求
,求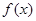 的最大值和最小值;
的最大值和最小值; ,求
,求 的值.
的值. ,
,
 且函数
且函数 的最小正周期为
的最小正周期为 .
. 的值和函数
的值和函数 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 、
、 、
、 ,又
,又 ,
, ,
, ,求边长
,求边长 、
、 、
、 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
 ,
,

 的大小;
的大小; 的距离.
的距离. 设函数
设函数 (Ⅰ)当
(Ⅰ)当 ,求函数
,求函数 的值域;
的值域; 的值;
的值;