题目内容
已知函数
(Ⅰ)若 ,求
,求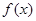 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若 ,求
,求 的值.
的值.
(1) 见解析;(2)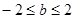 ;(3)见解析.
;(3)见解析.
解析试题分析:(1) 先将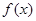 化为一角一函数形式,再根据正余弦函数的性质在定区间上求最值.此类题目必须将函数先化为一角一函数形式,化一角一函数的方法是对于函数
化为一角一函数形式,再根据正余弦函数的性质在定区间上求最值.此类题目必须将函数先化为一角一函数形式,化一角一函数的方法是对于函数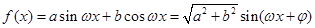 ,其中
,其中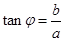 ;(ⅱ)根据(1)和条件
;(ⅱ)根据(1)和条件 ,求出
,求出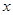 ,再将所求式子化简求值 .
,再将所求式子化简求值 .
试题解析:(I)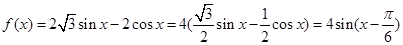 3分
3分
又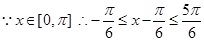 ,
,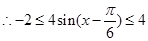
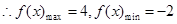 6分
6分
(II)由于 ,所以
,所以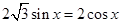 ,解得
,解得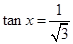 8分
8分
原式=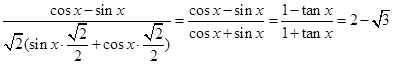 12分
12分
考点:1.两角和差的正弦公式;2.倍角公式;3.三角函数的性质.

练习册系列答案
相关题目
 .
. 的值;
的值;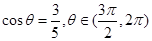 ,求
,求 .
. 的最大值为
的最大值为 ,最小值为
,最小值为 ,其中
,其中 .
. 表示);
表示); 的顶点与平面直角坐标系
的顶点与平面直角坐标系 中的原点
中的原点 重合,始边与
重合,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点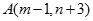 .求
.求 的值.
的值.  中,
中,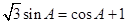 .
. 的大小;
的大小; 的取值范围.
的取值范围.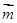 =(
=(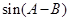 ,
,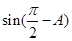 ),
),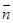 =(1,
=(1,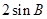 ),且
),且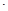
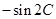 ,其中
,其中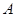 、
、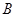 、
、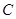 分别为
分别为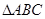 的三边
的三边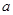 、
、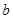 、
、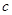 所对的角.
所对的角.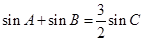 ,且
,且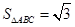 ,求边
,求边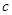 的长.
的长.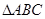 中,角
中,角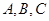 所对的边分别为
所对的边分别为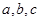 ,且
,且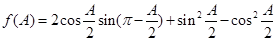 .
.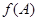 的最大值;
的最大值;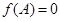 ,
,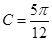 ,
,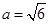 ,求
,求 的值.
的值.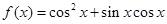 ,
,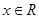
 的值;
的值;  ,且
,且 ,求
,求 .
.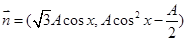 ,
,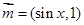 ,
,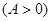 ,函数
,函数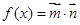 的最大值为
的最大值为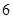 .
.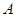 ;
;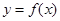 的图像向左平移
的图像向左平移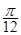 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的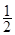 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数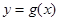 的图像,求
的图像,求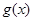 在
在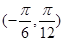 上的值域.
上的值域. .
. 的最小正周期;
的最小正周期;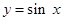 通过怎样的图像变换得到.
通过怎样的图像变换得到.