题目内容
已知函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)若数列![]() 满足:
满足:![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的通项
的通项![]() ;
;
(2)若数列![]() 满足:
满足:![]() ,
,![]() (
(![]() ).
).
①当![]() 时,数列
时,数列![]() 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列![]() 的通项
的通项![]() ;若不是,请说明理由;
;若不是,请说明理由;
②当![]() 时, 求证:
时, 求证:![]() .
.
解:(1)![]() ,
, ![]() ,
,
即![]()
![]() ,
, ![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
![]() ,即
,即![]() .
.
(2)①![]()
![]()
![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() .
.
假设![]() ,则
,则![]() .
.
由数学归纳法,得出数列![]() 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为![]() .
.
②![]() ,
, ![]() .
.
![]() 当
当![]() 时,
时,![]() .
.
假设![]() ,则
,则 ![]() .由数学归纳法,得出数列
.由数学归纳法,得出数列![]()
![]() .
.
又![]() ,
,
![]() ,即
,即![]() .
.
![]()
![]()
![]()
![]() .
.
![]() ,
,![]() .
.

练习册系列答案
相关题目
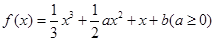 ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. ,
, 为函数
为函数 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间.