题目内容
已知直线l:x=my+1过椭圆(1)若直线l交y轴于点M,且![]() =λ1
=λ1![]() ,
,![]() =λ2
=λ2![]() ,当m变化时,求λ1+λ2的值;
,当m变化时,求λ1+λ2的值;
(2)连结AE、BD,试探索当m变化时,直线AE、BD是否相交于一点是N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由.
解:(1)由已知得M(0,![]() ),设A(x1,y1),B(x2,y2),由
),设A(x1,y1),B(x2,y2),由 得(3m2+4)y2+6my-6=0.
得(3m2+4)y2+6my-6=0.
∴y1+y2=![]() ,y1y2=
,y1y2=![]() .
.
由![]() =λ1
=λ1![]() ,得(x1,y1+
,得(x1,y1+![]() )=λ1(1-x1,-y1),
)=λ1(1-x1,-y1),
∴y1+![]() =-λ1y1.∴λ1=-1
=-λ1y1.∴λ1=-1![]() .同理λ2=-1
.同理λ2=-1![]() .
.
∴λ1+λ2=-2-![]() (
(![]() +
+![]() )=-2
)=-2![]() =-2+
=-2+![]() =
=![]() .
.
(2)当m=0时,A(1,![]() ),B(1,
),B(1,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() ).
).
∵ABED为矩形,∴N(![]() ,0).
,0).
当m≠0时,D(4,y1),E(4,y2),∵![]() =(
=(![]() -x1,-y1),
-x1,-y1),![]() =(
=(![]() ,y2),
,y2),
由(![]() -x1)y2+
-x1)y2+![]() y1=(
y1=(![]() -my1-1)y2+
-my1-1)y2+![]() y1=
y1=![]() (y1+y2)-my1y2=
(y1+y2)-my1y2=![]() +
+![]() =0.
=0.
∴![]() ∥
∥![]() ,即A、N、E三点共线.
,即A、N、E三点共线.
同理可证,B、N、D三点共线.综上,对任意m,直线AE、BD相交于定点N(![]() ,0).
,0).

练习册系列答案
相关题目
 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: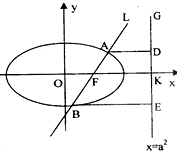 如图,已知直线L:
如图,已知直线L: