题目内容
5.已知角α的终边落在y=|2x|上,则cosα=±$\frac{\sqrt{5}}{5}$.分析 设出直线上点的坐标,可求cosα.
解答 解:角α终边在直线y=|2x|上,
所以在直线y=|2x|上取一个点A(1,2),则OA=$\sqrt{5}$,
所以,cosα=$\frac{\sqrt{5}}{5}$.
在直线y=2x上取一个点B(-1,2),OB=$\sqrt{5}$,
所以,cosα=-$\frac{\sqrt{5}}{5}$.
故答案为:±$\frac{\sqrt{5}}{5}$.
点评 本题考查终边相同的角,任意角的三角函数的定义,计算能力,是基础题.

练习册系列答案
相关题目
16.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=$\frac{2}{x}$ | B. | y=$lo{g}_{\frac{1}{2}}$|x| | C. | y=x2+2 | D. | y=-2x+5 |
13.随机事件A的频率$\frac{m}{n}$满足( )
| A. | $\frac{m}{n}=0$ | B. | $\frac{m}{n}=1$ | C. | 0$<\frac{m}{n}<1$ | D. | 0$≤\frac{m}{n}≤1$ |
20.若sinθ=$\frac{3}{5}$,且cosθ=-$\frac{4}{5}$,则θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
14.i是虚数单位,设复数z满足|z|=1,则|$\frac{{z}^{2}-2z+2}{z-1+i}$|的最大值为( )
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | 2+$\sqrt{2}$ |
15.已知log${\;}_{\frac{1}{2}}$b<-log2a<-2log4c,则( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>b>c |
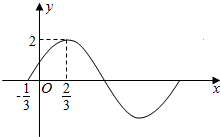 己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.