题目内容
已知平面内三点A(-1,0),B(x,6),P(3,4),且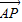 =λ
=λ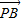 ,x和λ的值分别为( )
,x和λ的值分别为( )A.-7,2
B.5,2
C.-7,

D.5,

【答案】分析:利用向量的坐标运算和向量共线定理即可得出.
解答:解:∵平面内三点A(-1,0),B(x,6),P(3,4),∴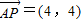 ,
,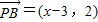 ,
,
∵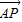 =λ
=λ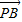 ,
,
∴(4,4)=λ(x-3,2),∴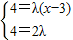 ,解得
,解得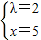 .
.
∴x和λ的值分别为5,2.
故选B.
点评:熟练掌握向量的坐标运算和向量共线定理是解题的关键.
解答:解:∵平面内三点A(-1,0),B(x,6),P(3,4),∴
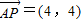 ,
,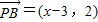 ,
,∵
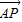 =λ
=λ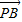 ,
,∴(4,4)=λ(x-3,2),∴
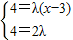 ,解得
,解得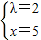 .
.∴x和λ的值分别为5,2.
故选B.
点评:熟练掌握向量的坐标运算和向量共线定理是解题的关键.

练习册系列答案
相关题目
已知平面内三点A(2,2),B(1,3),C(7,x)满足
⊥
,则x的值为( )
| BA |
| AC |
| A、3 | B、6 | C、7 | D、9 |