题目内容
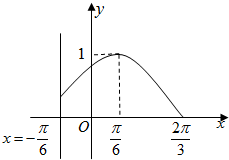 已知定义在区间[-π,
已知定义在区间[-π,| 2 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
(Ⅰ)求函数y=f(x)在[-π,
| 2 |
| 3 |
(Ⅱ)求方程f(x)=
| ||
| 2 |
分析:( I)由图象可知A=1,依题意解方程组
可求得ω与φ,从而可求得y=f(x)在[-π,
π]上的表达式;
(Ⅱ)f(x)=
,利用正弦函数的性质先在区间x∈[-
,
]上求得x的值,再利用y=f(x)关于x=-
对称,求得x∈[-π,-
]上求得x的值.
|
| 2 |
| 3 |
(Ⅱ)f(x)=
| ||
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
解答:解:( I)由图象可知A=1,ω>0,-
<φ<
,有
(2分)
解得:
,
所以x∈[-
,
]时,f(x)=sin(x+
).(3分)
由y=f(x)关于直线x=-
对称,可求的得当x∈[-π,-
]时,f(x)=-sinx.(5分)
综上,f(x)=
(6分)
( II)因为f(x)=
,则在区间x∈[-
,
]上有:x+
=
或x+
=
,(8分)
所以x1=0,x2=
.(10分)
又y=f(x)关于x=-
对称,
所以x3=-
,x4=-
也是方程的解,(11分)
所以方程f(x)=
的解为x=-
,-
,0,
.(12分)
| π |
| 2 |
| π |
| 2 |
|
解得:
|
所以x∈[-
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
由y=f(x)关于直线x=-
| π |
| 6 |
| π |
| 6 |
综上,f(x)=
|
( II)因为f(x)=
| ||
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
所以x1=0,x2=
| π |
| 3 |
又y=f(x)关于x=-
| π |
| 6 |
所以x3=-
| π |
| 3 |
| 2π |
| 3 |
所以方程f(x)=
| ||
| 2 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查直线与正弦曲线的位置关系,考查对称问题,属于难题.

练习册系列答案
相关题目
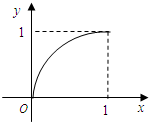 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: