题目内容

长方形ABCD中，AB=2，BC=1，O为AB的中点，在长方形ABCD内随机取一点，取到的点到O的距离大于1的概率为
 
．
分析：本题利用几何概型解决，这里的区域平面图形的面积．欲求取到的点到O的距离大于1的概率，只须求出圆外的面积与矩形的面积之比即可．
解答：解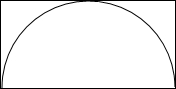：精英家教网根据几何概型得：
取到的点到O的距离大于1的概率：
p=
d
D
=
圆外部分的面积
矩形的面积

=
2-
π
2
2×1
=1-
π
4
．
故答案为：1-
π
4
点评：本题主要考查几何概型．如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
相关题目
在长方形ABCD中，AB=2，AD=1，则
AC
•
CD
=（　　）
如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．

（1）求证：AD⊥BM；
（2）点E是线段DB上的一动点，当二面角A-EM-D大小为
π
3
时，试求
DE
DB
的值．
如图在长方形ABCD中，AB=
3
，BC=1，E为线段DC上一动点，现将△AED沿AE折起，使点D在面ABC上的射影K在直线AE上，当E从D运动到C，则K所形成轨迹的长度为（　　）
在长方形ABCD中，AB=2，BC=1，O为AB中点，在长方形ABCD内随机取一点，取到的点到点O的距离不大于1的概率是（　　）
（2013•揭阳二模）在图（1）所示的长方形ABCD中，AD=2AB=2，E、F分别为AD、BC的中点，M、N两点分别在AF和CE上运动，且AM=EN=a(0＜a＜
2
)．把长方形ABCD沿EF折成大小为θ的二面角A-EF-C，如图（2）所示，其中θ∈(0，
π
2
]
（1）当θ=45°时，求三棱柱BCF-ADE的体积；
（2）求证：不论θ怎么变化，直线MN总与平面BCF平行；
（3）当θ=900且a=
2
2
．时，求异面直线MN与AC所成角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网