题目内容
如图,点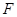 是椭圆
是椭圆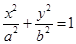 (
(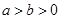 )的左焦点,点
)的左焦点,点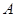 ,
,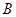 分别是椭圆的左顶点和上顶点,椭圆的离心率为
分别是椭圆的左顶点和上顶点,椭圆的离心率为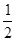 ,点
,点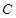 在
在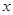 轴上,且
轴上,且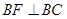 ,过点
,过点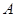 作斜率为
作斜率为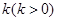 的直线
的直线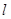 与由三点
与由三点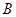 ,
,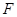 ,
,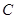 确定的圆
确定的圆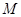 相交于
相交于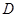 ,
,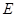 两点,满足
两点,满足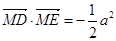 .
.
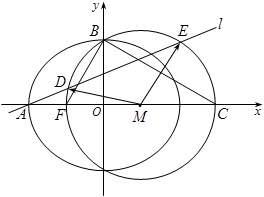
(1)若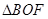 的面积为
的面积为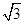 ,求椭圆的方程;
,求椭圆的方程;
(2)直线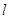 的斜率是否为定值?证明你的结论.
的斜率是否为定值?证明你的结论.
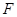 是椭圆
是椭圆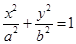 (
(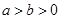 )的左焦点,点
)的左焦点,点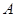 ,
,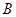 分别是椭圆的左顶点和上顶点,椭圆的离心率为
分别是椭圆的左顶点和上顶点,椭圆的离心率为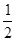 ,点
,点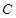 在
在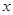 轴上,且
轴上,且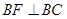 ,过点
,过点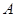 作斜率为
作斜率为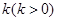 的直线
的直线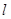 与由三点
与由三点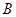 ,
,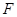 ,
,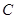 确定的圆
确定的圆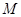 相交于
相交于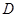 ,
,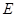 两点,满足
两点,满足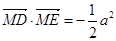 .
.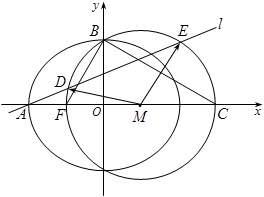
(1)若
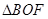 的面积为
的面积为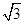 ,求椭圆的方程;
,求椭圆的方程;(2)直线
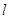 的斜率是否为定值?证明你的结论.
的斜率是否为定值?证明你的结论. (1)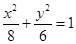
(2)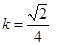
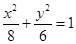
(2)
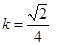
试题分析:解:(1)由已知可得
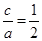 ,
, 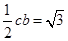 , 2分
, 2分又
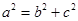 ,
,解得
 . 3分
. 3分所求椭圆方程为
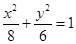 . 4分
. 4分(2)由
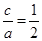 得
得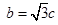 ,则
,则 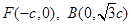 5分
5分因
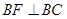 则
则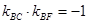 (斜率显然存在且不为零) 6分
(斜率显然存在且不为零) 6分而
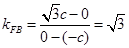
设
 ,则
,则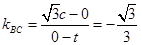
得
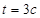 ,所以
,所以 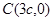 7分
7分 则圆心
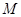 的坐标为
的坐标为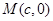 ,半径为
,半径为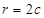 8分
8分据题意 直线
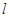 的方程可设为
的方程可设为 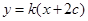 ,即
,即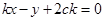 9分
9分由
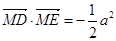 得
得 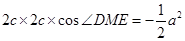 10分
10分即
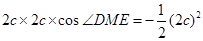 ,得
,得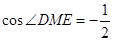 ,而
,而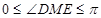
所以
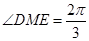 11分
11分在等腰三角形
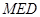 中 由垂径定理可得点
中 由垂径定理可得点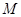 到直线
到直线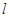 的距离为
的距离为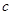 . 12分
. 12分则
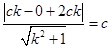 13分
13分解得
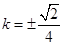 而
而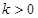 故
故 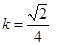 (定值) 14分
(定值) 14分点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
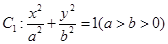 的离心率为
的离心率为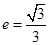 ,直线
,直线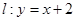 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆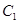 的短半轴长为半径的圆
的短半轴长为半径的圆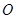 相切.
相切.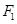 ,右焦点为
,右焦点为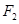 ,直线
,直线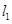 过点
过点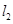 垂直于
垂直于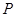 ,线段
,线段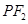 的垂直平分线交
的垂直平分线交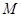 ,求点
,求点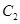 的方程;
的方程;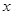 轴交于点
轴交于点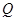 ,不同的两点
,不同的两点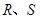 在
在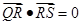 ,求
,求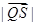 的取值范围.
的取值范围.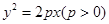 的焦点
的焦点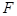 恰为双曲线
恰为双曲线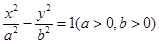 的右焦点,且两曲线交点的连线过点
的右焦点,且两曲线交点的连线过点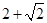
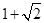
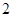
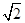
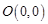 ,
,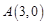 ,动点
,动点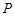 到定点
到定点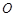 距离与到定点
距离与到定点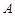 的距离的比值是
的距离的比值是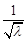 .
.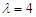 时,记动点
时,记动点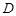 .
. 是圆
是圆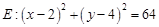 上任意一点,过
上任意一点,过 ,求
,求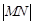 的取值范围;
的取值范围;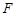 ,
,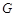 是曲线
是曲线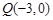 ,有
,有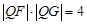 .试问无论
.试问无论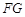 能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.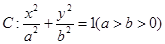 的离心率为
的离心率为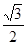 ,双曲线
,双曲线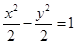 的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )
的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )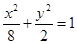
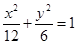
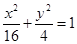
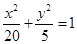
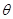 ,
, 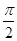 ), 以A, B为焦点且过点D的双曲线的离心率为e1, 以C, D为焦点且过点A的椭圆的离心率为e2, 设
), 以A, B为焦点且过点D的双曲线的离心率为e1, 以C, D为焦点且过点A的椭圆的离心率为e2, 设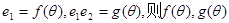
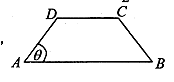
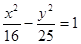 的左焦点为
的左焦点为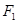 ,点
,点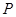 为双曲线右支上一点,且
为双曲线右支上一点,且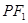 与圆
与圆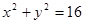 相切于点
相切于点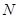 ,
,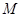 为线段
为线段 为坐标原点, 则
为坐标原点, 则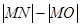 =
= 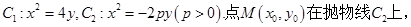

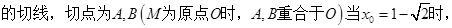
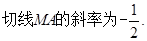
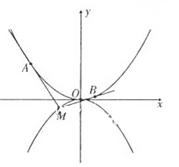
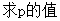 ;
;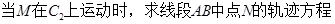

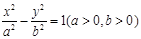 与抛物线
与抛物线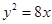 有一个公共的焦点
有一个公共的焦点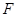 ,且两曲线的一个交点为
,且两曲线的一个交点为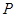 ,若
,若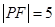 ,则双曲线的渐近线方程为 .
,则双曲线的渐近线方程为 .