Question

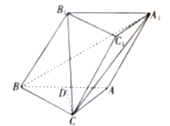
【题目】已知三棱柱，平面，P是内一点，点E，F在直线上运动，若直线和所成角的最小值与直线和平面所成角的最大值相等，则满足条件的点P的轨迹是（ ）

A.圆的一部分B.椭圆的一部分C.抛物线的一部分D.双曲线的一部分

Answer 1

【答案】C

【解析】

由题意可知到的距离等于到的距离，故而到的距离等于到的距离，得出结论.

设三棱柱的高为在平面上的射影为，

则当共线时，直线和所成角取得最小值，

不妨设最小值为，则，

当时，直线和平面所成角取得最大值，

不妨设最大值为，则，

∴当直线和所成角的最小值与直线和平面所成角的最大值相等时，

，即到的距离等于到直线的距离，

设到的距离为，则，

∴到的距离等于到的距离，

∴的轨迹是以为焦点，以为准线的抛物线的一部分，

故选：C.