题目内容
把函数f(x)=sin2x-2sinxcosx+3cos2x的图象沿x轴向左平移m(m>0)个单位,所得函数的图象关于直线x=(1)求m的最小值;
(2)证明当x∈(-![]() π,-
π,-![]() π)时,经过函数f(x)图象上任意两点的直线的斜率恒为负数;
π)时,经过函数f(x)图象上任意两点的直线的斜率恒为负数;
(3)设x1,x2∈(0,π),x1≠x2,且f(x1)=f(x2)=1,求x1+x2的值.
分析:(1)f(x)的图象平移后关于直线x=![]() π对称,则x=
π对称,则x=![]() π使平移后的函数式取最值;(2)只需计算图象上任两点斜率的范围;(3)可求出x1,x2的值即可.
π使平移后的函数式取最值;(2)只需计算图象上任两点斜率的范围;(3)可求出x1,x2的值即可.
解:(1)f(x)=sin2x-2sinxcosx+3cos2x=![]() -sin2x+3·
-sin2x+3·![]()
=cos2x-sin2x+2=![]() cos(2x+
cos(2x+![]() )+2.
)+2.
将f(x)的图象沿x轴向左平移m个单位得到函数g(x)=![]() cos[2(x+m)+
cos[2(x+m)+![]() ]+2的图象.
]+2的图象.
∵g(x)的图象关于直线x=![]() π对称,∴2(
π对称,∴2(![]() π+m)+
π+m)+![]() =kπ(k∈Z)即m=
=kπ(k∈Z)即m=![]() (k∈Z),又m>0,∴m的最小值为
(k∈Z),又m>0,∴m的最小值为![]() (k=5时取得).
(k=5时取得).
(2)∵-![]() π<x<-
π<x<-![]() π,∴-4π<2x+
π,∴-4π<2x+![]() <-
<-![]() π,∴f(x)在(-
π,∴f(x)在(-![]() π,-
π,-![]() π)上是减函数.于是x1,x2∈(-
π)上是减函数.于是x1,x2∈(-![]() π,-
π,-![]() π),且x1<x2,便有f(x1)>f(x2)从而经过两点(x1,f(x1),(x2,f(x2))的斜率k=
π),且x1<x2,便有f(x1)>f(x2)从而经过两点(x1,f(x1),(x2,f(x2))的斜率k=![]() <0.
<0.
(3)f(x)=1![]() cos(2x+
cos(2x+![]() )=-
)=-![]() ,在(0,π)内满足cos(2x+
,在(0,π)内满足cos(2x+![]() )=-
)=-![]() 的值为
的值为![]() 和
和![]() .∵f(x1)=f(x2)=1.且x1,x2∈(0,π).x1≠x2,∴x1+x2=
.∵f(x1)=f(x2)=1.且x1,x2∈(0,π).x1≠x2,∴x1+x2=![]() +
+![]() =
=![]() π
π
另法:由2x+![]() =kπ(k∈Z)得x=
=kπ(k∈Z)得x=![]() -
-![]()
∴在(0,π)内的对称轴为x=![]() π和x=
π和x=![]() π
π
又f(x1)=f(x2)=1,且x1,x2∈(0,π).x1≠x2,x∈(![]() π,π)时f(x)≠1.
π,π)时f(x)≠1.
∴x1+x2=2×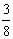 π=
π=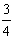 π.
π.

练习册系列答案
相关题目