题目内容
已知定义在(0,+∞)上的单调函数f(x),对∀x∈(0,+∞),都有f[f(x)-log3x]=4,则函数g(x)=f(x-1)-f′(x-1)-3的零点所在区间是( )
A.(1,2) B.(2,3)
C.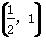 D.
D.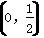
B
[解析] 由题意,得f(x)-log3x=c(c为常数),则f(x)=log3x+c,故f[f(x)-log3x]=f(c)=log3c+c=4.∴c=3,∴f(x)=log3x+3,则函数g(x)=f(x-1)-f′(x-1)-3=log3(x-1)- log3e在(1,+∞)上为增函数,又g(2)=-log3e<0,g(3)=log32-
log3e在(1,+∞)上为增函数,又g(2)=-log3e<0,g(3)=log32-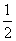 log3e>0,故函数g(x)=f(x-1)-f′(x-1)-3的零点所在的区间是(2,3),故选B.
log3e>0,故函数g(x)=f(x-1)-f′(x-1)-3的零点所在的区间是(2,3),故选B.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 中,
中, 分别是
分别是 的中点,则直线
的中点,则直线 与平面
与平面 所成角的正切值为 (D )
所成角的正切值为 (D ) B.
B. C.
C. D.
D.
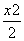 +y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________.
+y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|取最大值时,点P的坐标为________.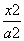 +
+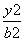 =1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=
=1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cos α=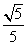 ,sin(α+β)=
,sin(α+β)=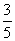 ,则此椭圆的离心率为________.
,则此椭圆的离心率为________.

 dx=3+ln 2(a>1),则a的值为( )
dx=3+ln 2(a>1),则a的值为( ) 满足
满足 ,且
,且 ,则向量
,则向量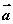 与
与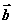 的夹角是( )
的夹角是( )
 的最小正周期、最大值和最小值;
的最小正周期、最大值和最小值;