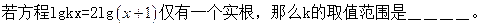题目内容
设f(x)是定义在区间 上以2为周期的函数,对
上以2为周期的函数,对 ,用
,用 表示区间
表示区间 已知当
已知当 时,f(x)=x2.
时,f(x)=x2.
(1)求f(x)在 上的解析表达式;
上的解析表达式;
(2)对自然数k,求集合 不等的实根}
不等的实根}
 上以2为周期的函数,对
上以2为周期的函数,对 ,用
,用 表示区间
表示区间 已知当
已知当 时,f(x)=x2.
时,f(x)=x2.(1)求f(x)在
 上的解析表达式;
上的解析表达式;(2)对自然数k,求集合
 不等的实根}
不等的实根}(1)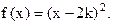 (2)
(2)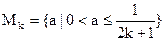
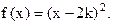 (2)
(2)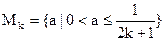
解:(1)∵f(x)是以2为周期的函数,∴当 时,2k也是f(x)的周期
时,2k也是f(x)的周期
又∵当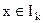 时,
时,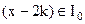 ,∴
,∴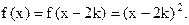
即对 ,当
,当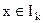 时,
时,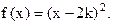
(2)当 且
且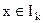 时,利用(1)的结论可得方程
时,利用(1)的结论可得方程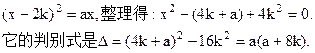
上述方程在区间 上恰有两个不相等的实根的充要条件是a满足
上恰有两个不相等的实根的充要条件是a满足
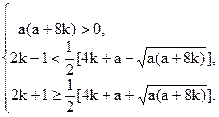
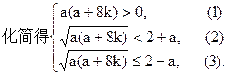
由(1)知a>0,或a<-8k.
当a>0时:因2+a>2-a,故从(2),(3)
可得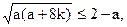 即
即
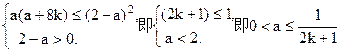
当a<-8k时: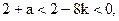
易知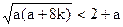 无解,
无解,
综上所述,a应满足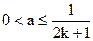 故所求集合
故所求集合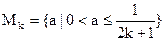
 时,2k也是f(x)的周期
时,2k也是f(x)的周期
又∵当
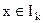 时,
时,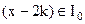 ,∴
,∴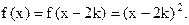
即对
 ,当
,当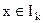 时,
时,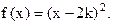
(2)当
 且
且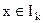 时,利用(1)的结论可得方程
时,利用(1)的结论可得方程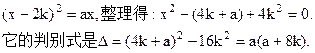
上述方程在区间
 上恰有两个不相等的实根的充要条件是a满足
上恰有两个不相等的实根的充要条件是a满足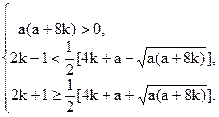
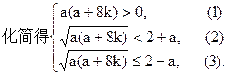
由(1)知a>0,或a<-8k.
当a>0时:因2+a>2-a,故从(2),(3)
可得
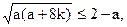 即
即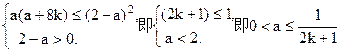
当a<-8k时:
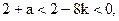
易知
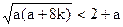 无解,
无解,综上所述,a应满足
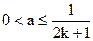 故所求集合
故所求集合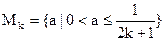

练习册系列答案
相关题目
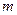 为何值时,关于
为何值时,关于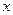 的方程
的方程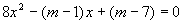 的两根:
的两根: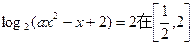 内有解,实数a的取值范围.
内有解,实数a的取值范围.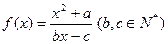 ,若方程
,若方程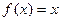 有且只有两个相异根0和2,且
有且只有两个相异根0和2,且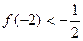 (1)求函数
(1)求函数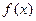 的解析式。(2)已知各项不为1的数列{an}满足
的解析式。(2)已知各项不为1的数列{an}满足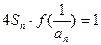 ,求数列通项an。(3)如果数列{bn}满足
,求数列通项an。(3)如果数列{bn}满足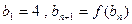 ,求证:当
,求证:当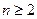 时,恒有
时,恒有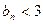 成立。
成立。 的一个零点在
的一个零点在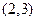 内,则实数
内,则实数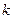 的取值范围是( )
的取值范围是( )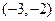
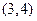
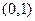
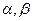 是方程
是方程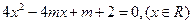 的两实根,当
的两实根,当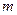 为何值时,
为何值时,
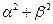 有最小值?求出这个最小值.
有最小值?求出这个最小值.