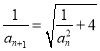题目内容
【题目】已知双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,若在线段
为虚轴的一个端点,若在线段![]() 上(不含端点)存在两点
上(不含端点)存在两点![]() ,使得
,使得![]() ,则双曲线的渐近线斜率
,则双曲线的渐近线斜率![]() 的平方的取值范围是( )
的平方的取值范围是( )
A.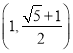 B.
B.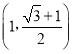 C.
C.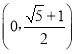 D.
D.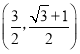
【答案】A
【解析】
根据题意可知,若在线段![]() 上(不含端点)存在两点
上(不含端点)存在两点![]() ,使得
,使得![]() ,则以
,则以![]() 为直径的圆与直线
为直径的圆与直线![]() 相交,利用直线与圆的位置关系和点到直线距离公式求解.
相交,利用直线与圆的位置关系和点到直线距离公式求解.
双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,
为虚轴的一个端点,
则可得![]() ,
,![]()
则直线![]() 的方程为
的方程为![]()
若在线段![]() 上(不含端点)存在两点
上(不含端点)存在两点![]() ,使得
,使得![]() ,
,
则以![]() 为直径的圆与直线
为直径的圆与直线![]() 相交,
相交,
圆的方程和半径分别为![]() ,
,
所以满足圆心到直线![]() 的距离小于半径,即
的距离小于半径,即 ,
,
化简可得![]() ,
,
又因为![]() ,代入上式化简可得
,代入上式化简可得![]() ,
,
将不等式两边同时除以![]() 可得
可得 ,
,
令 ,上述不等式可化为
,上述不等式可化为![]()
令![]() 解得
解得![]() ,
,![]() (舍),
(舍),
所以![]() 的解集为
的解集为![]() ,即
,即 ,
,
因为两个交点位于线段![]() 上(不含端点),
上(不含端点),
所以![]() ,即
,即![]() ,
,
综上可知 ,
,
故选:A.

练习册系列答案
相关题目